Problems with every day objects (repost): Baby Building Blocks

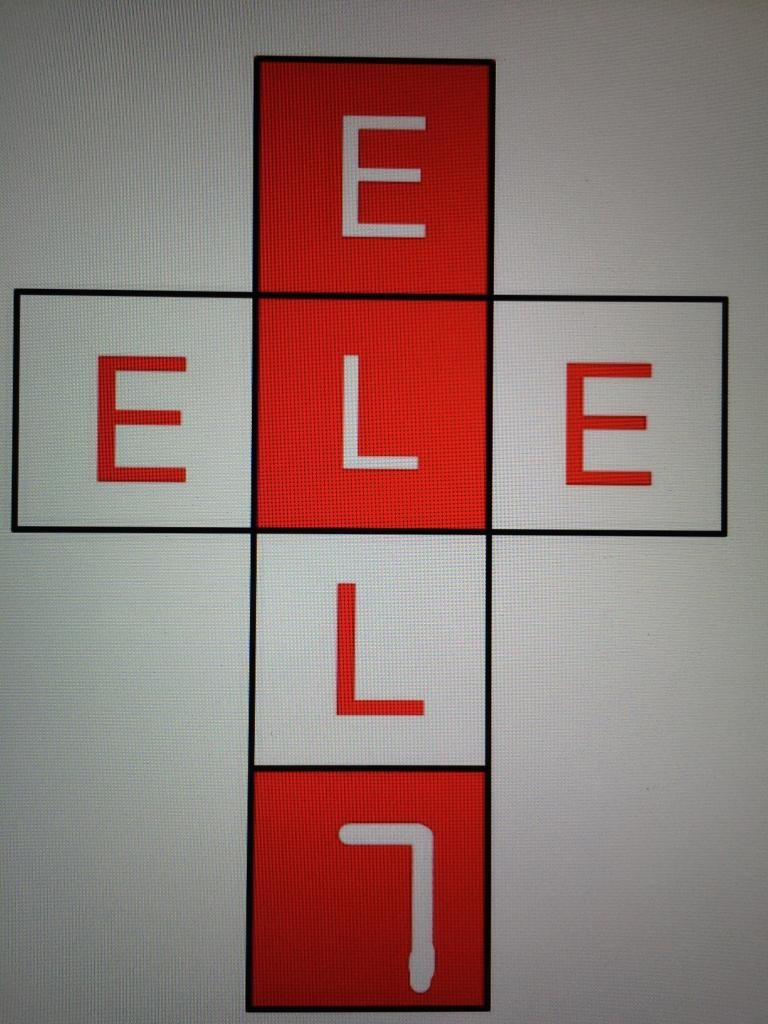
Cube Net depicted above
Today, while sitting in the doctors office waiting, I saw four identical cubes with 3 white and 3 red faces. I couldn't help myself so I began to play with them... And by play with them, I mean that I began to make a math problem about how many arrangements I could make with them. So here it is:
When lined up side by side and only looking at the top face of each cube. How many different arrangements of the identical cubes can I make such that there is no rotational symmetry along the x,y, or z axis or around the origin.
Assume:
The origin is the center of the 4x1x1 rectangular prison formed by aligning the four blocks.
If the letters have the same orientation and order as another combination but has a different color order, it's considered different and does not have reflectional symmetry.
Hint: if the top of the four blocks are in this specific order it is rotationally symmetric Around the y axis.
The answer is 65280.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
This problem doesnt require much computation or much of any thing else. Except for a change of perspective.
Rather than over complicating things, lets look at this from a 2D perspective. We don't have to look at the 3D space because if the arrangement of cubes is rotationally symmetrical (they will actually never be reflectionally symmetric), then the arrangement of every face of the 4x1 rectangular prism (formed by aligning the 4 blocks) will be rotationally symmetric.
Say we are looking at the top block. Now, imagine separating the cube layout to the 4 distinct faces (red E, white E, red L, white L) and making them into separate squares.
We will substitute letters for each orientation of each square. The first column is the letter/number displayed on the square and the second/third represent the color of that letter. (Sorry for the horrible 2nd and 4th columns, those represent an L rotated 90 degrees clock wise and counter clock wise.
\begin{array}{l|c|r}\text{Number/character} & \text{red L/E} & \text{white L/E} \\ \hline \underline{~~}\underline{~~}\underline{~~} | & B & F \\ \hline L & A & E \\ \hline 7 &C&G \\ \hline \overline{\color \white{l}}\overline{\color \white{l}}\overline{\color \white{l}}|&D&H \\ \hline E&1&5 \\ \hline ᵚ&2&6 \\ \hline ∃&3&7 \\ \hline m&4&8 \end{array}
We can clearly see that we have 16 distinct objects. Each which can be placed in one space.
This means that there are 1 6 ⋅ 1 6 ⋅ 1 6 ⋅ 1 6 = 1 6 4 orientations. Now, for them to be rotationally symmetrical, we need to look at each letter being rotated 180 degrees. Thus by 180 deg rotation.
a=c
b=d
e=g
f=h
1=3
2=4
5=7
6=8.
Or in other words, for each ordering of two squares, there is exactly one pair of squares that will match it when rotated 180 degrees.
Therefore, we must subtract 1 for each ordering of two squares, which is 1 6 ∗ 1 6 = 1 6 2
Thus our final answer is 1 6 4 − 1 6 2 = 6 5 2 8 0