Problems with everyday objects: the tear drop
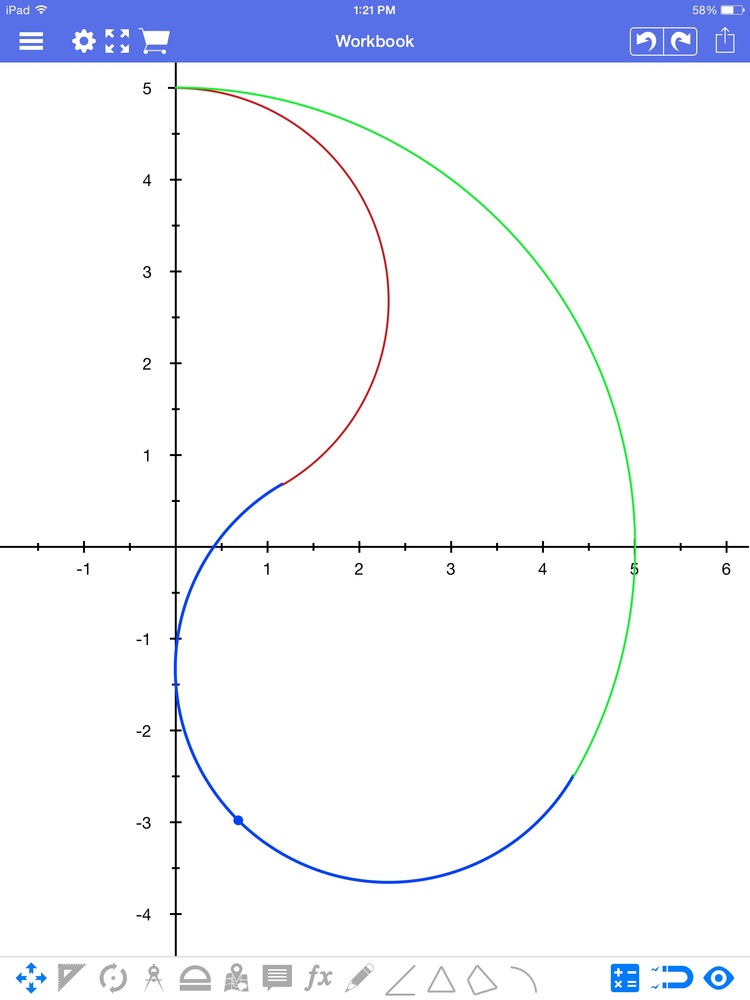
Find the area A of the tear drop graphed above.
Input your answer as ⌊ 1 0 0 A ⌋ , where ⌊ x ⌋ is the greatest integer function (the greatest integer less than or equal to x).
Assume:
The red curve is defined by the function x 2 + ( y − 2 0 + 1 0 3 ) 2 = ( 1 0 3 − 1 5 ) 2
The blue curve is defined by the function ( x − 1 0 3 + 1 5 ) 2 + ( y + 1 0 − 5 3 ) 2 = ( 1 0 3 − 1 5 ) 2
The green curve is defined by the function x 2 + y 2 = 2 5 .
The blue curve ends at its point of tangency with the red curve and green curve
Each curve begins and ends at a point of tangency.
The answer is 2589.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
I really like how there is a long chain of 0 s at the decimal part:
25.8905000093356
Answer is correct but some steps are missed .
A
r
e
a
o
f
b
i
g
c
i
r
c
l
e
=
2
5
∗
π
.
=
7
8
.
5
3
9
8
.
A
r
e
a
o
f
Δ
=
4
3
∗
{
2
∗
(
1
0
3
−
1
5
)
}
2
=
9
.
3
2
6
7
.
A
r
e
a
o
f
t
h
r
e
e
s
e
c
t
o
r
s
=
2
π
∗
(
1
0
3
−
1
5
)
2
=
8
.
4
5
8
S
o
t
h
e
a
r
e
a
o
f
s
i
n
g
l
e
=
3
7
8
.
5
3
9
8
−
(
9
.
3
2
6
7
−
8
.
4
5
8
4
)
=
2
5
.
8
9
.
S
o
o
u
r
a
n
s
w
e
r
i
s
3
1
∗
{
2
5
π
−
(
4
3
∗
{
2
∗
(
1
0
3
−
1
5
)
}
2
−
2
π
∗
(
1
0
3
−
1
5
)
2
)
}
=
2
5
.
8
9
0
.
Thank you. Up till now I was dividing a problem and solving the simple small part. You taught me that at times combining several parts makes the solution easy. Up voted.
After rotating the image and making three copies of it, we achieve the first picture.
We can complete the arcs to make three circles whose centers are connected by an equilateral triangle. Which is the second picture.
To find the area of the curved triangle in the middle, we take the area of the equilateral triangle and subtract 3 times 1/6 the area of one of th espalier circles. The area of one of those circles is ( 1 0 3 − 1 5 ) 2 π , so we are subtracting 2 ( 1 0 3 − 1 5 ) 2 π
After subtracting the area of this curvy triangle, we subtract it's area from the larger circle and divide that by 3 since there are 3 tear drops that are all congruent.
So our answer is 3 2 5 π − ( 2 ( 1 0 3 − 1 5 ) 2 π ) ≈ 2 5 . 8 9 0
So ⌊ ( 2 5 . 8 9 0 ) ( 1 0 0 ) ⌋ = 2 5 8 9