Product of Digits

$For\quad digits\quad from\quad 1\quad to\quad 9,\quad the\quad sum\quad is:-\\ \\ 1\quad +\quad 2\quad +\quad 3\quad +\quad 4\quad +\quad 5\quad +\quad 6\quad +\quad 7\quad +\quad 8\quad +\quad 9\quad \\ \\ Next,\quad for\quad 10\quad to\quad 19:-\\ \\ 1\quad +\quad 1\quad +\quad 2\quad +\quad 3\quad +\quad 4\quad +\quad 5\quad +\quad 6\quad +\quad \\ 7\quad +\quad 8\quad +\quad 9\quad \\ \\ Then\quad for\quad 20\quad to\quad 29:-\\ \\ 2(\quad 1\quad +\quad 1\quad +\quad 2\quad +\quad 3\quad +\quad 4\quad +\quad 5\quad +\quad 6\quad \\ +\quad 7\quad +\quad 8\quad +\quad 9)\\ \\ And\quad so\quad on\quad till\quad 99.\\ \\ Thus,\quad let's\quad take\quad S\quad =\quad 1\quad +\quad 1\quad +\quad 2\quad +\quad 3\quad +\quad 4\quad +\quad 5\quad \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad +\quad 6\quad +\quad 8\quad +\quad 9\\ \\ Thus,\quad for\quad digits\quad till\quad 99\quad we\quad have.\\ \\ S\quad +\quad S\quad +\quad 2S\quad +\quad 3S\quad +\quad 4S\quad +\quad 5S\quad +\quad 6S\quad +\quad 7S\\ +8S\quad +\quad 9S\quad =\quad 46S\\ \\ Now\quad for\quad 100\quad to\quad 999:-\\ \\ \quad 1\quad \times \quad 1\quad \times \quad S\\ +1\quad \times \quad 2\quad \times \quad S\\ .\\ .\\ .\\ +1\quad \times \quad 9\quad \times \quad S\\ +2\quad \times \quad 1\quad \times \quad S\\ +2\quad \times \quad 2\quad \times \quad S\\ .\\ .\\ .\\ +9\quad \times \quad 9\quad \times \quad S\\ \\ Adding\quad all,\quad we\quad get:-\\ (46\quad \times \quad 46\quad \times \quad S)\quad -\quad 1\quad (Because\quad there's\quad one\quad 1\quad less\\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad in\quad first\quad in\quad first\quad step)\\ =\quad { 46 }^{ 3 }\quad -\quad 1\\ =\quad \boxed { 97335 }$

I worked out the answer but I couldnt resist to work out for the general case, and the result is beautiful, here it goes

sum |n= 1 to 999 P(n)

can be be written as

sum |n= 1 to 10^3 - 1 P(n)

or in general sum |i = 1 to 10^n - 1 P(i), where n> 0

then, sum |i = 1 to 10^n - 1 P(i) = 45* { sum |j=0 to n-1 (46^j-1) }

or simply

sum |i = 1 to 10^n - 1 P(i) = 45*(1 + 46 + 46^2 + ...... + 46^n-1)

example:
sum |i = 1 to 9 P(i) = 45*(1) = 45

sum |i = 1 to 99 P(i) = 45*(1 + 46^1) = 2115

sum |i = 1 to 999 P(i) = 45*(1 + 46^1 + 46^2) = 97335 (Current Problem)

sum |i = 1 to 9999 P(i) = 45*(1 + 46^1 + 46^2 + 46^3) = 4477455

sum |i = 1 to 99999 P(i) = 45*(1 + 46^1 + 46^2 + 46^3 + 46^4) = 205962975

sum |i = 1 to 999999 P(i) = 45*(1 + 46^1 + 46^2 + 46^3 + 46^4 + 46^5) = 9474296895

.

.

.

sum |i = 1 to 10^n -1 P(i) = 45*(1 + 46^1 + 46^2 + .......46^n-1) - General case

It can also be shown that all sums are mulitples of 9

Brock probably should use the above formula on his program, to save a lot of his computational power, resource and time.

45+(1+45) ((45+2) 45)

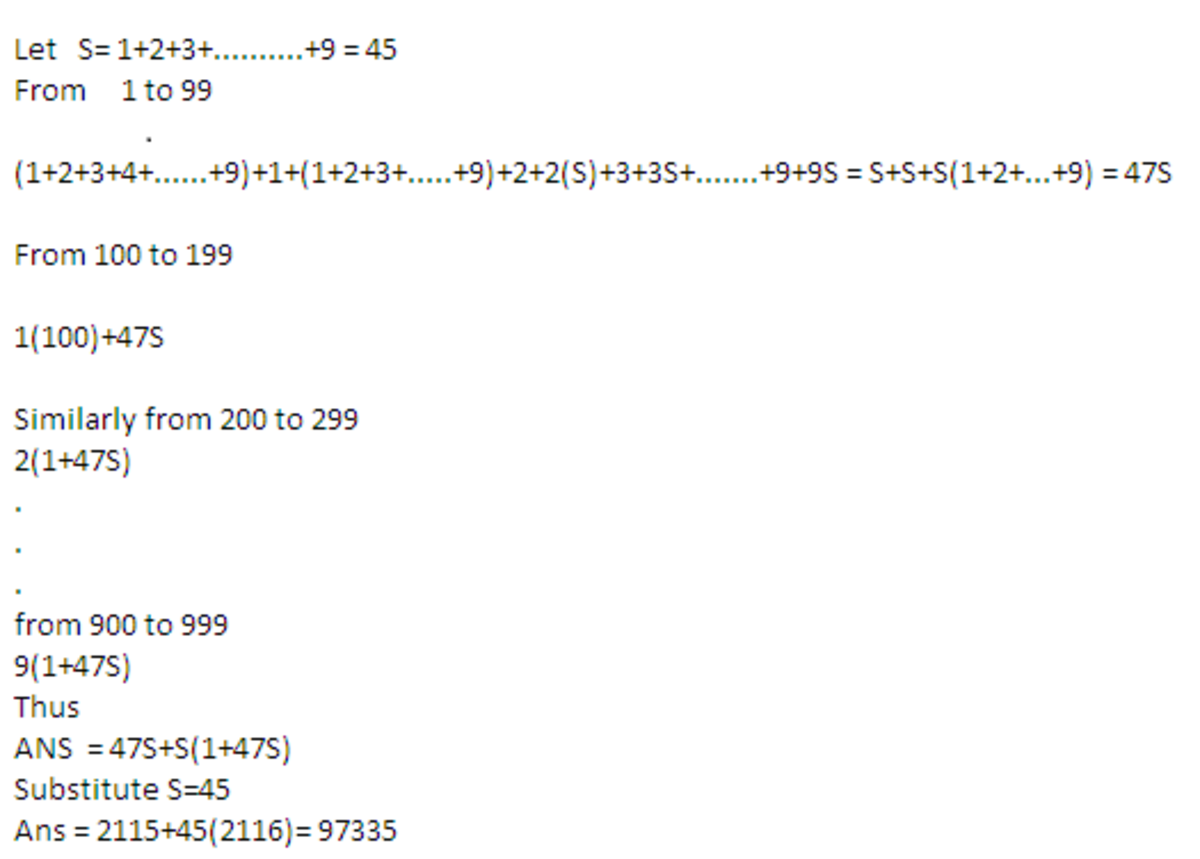
Let $S=1+2+3+4+5+6+7+8+9=45$

$(1+2+3+4+5+6+7+8+9) \times (1+2+3+4+5+6+7+8+9)$

It forms all the possible combinations of the two digit expect the ones with
zeroes . $(1 \times 9 \quad means \quad 19 \quad and \quad 9\times 1\quad means\quad product \quad of \quad digits \quad of \quad 91)$

Now the one with zeroes there are two possible cases that is zero at tens place(single digit integer) or at units place . In both case the sum is $S$ .

So the sum of products for two digit nos is $(S^2+2 S)= \boxed{2115 }$

For the three digit numbers

$(1+2+3+4+5+6+7+8+9) \times (1+2+3+4+5+6+7+8+9) \times (1+2+3+4+5+6+7+8+9)$

$(9 \times 9 \times 3 \quad means\quad product \quad of \quad digits \quad of \quad 993)$

forms all the possible combinations of the three digit nos expect the ones with
zeroes .

if there is one zero it can come at units place or tens for both the cases

the sum will be $S^2$ like mentioned above

when there are two zeroes the sum will be $S$ $(case \quad includes \quad 100,200........900)$ .

total sum for three digit numbers is $S^3+2S^2+S=\boxed{95220}$

Therefore the total sum is $2115+95220=97335$

Python:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

def p(n):
    product = 1
    for digit in str(n):
        if digit != '0':
            product *= int(digit)
    return product
total = 0
for n in xrange(1,1000):
    total += p(n)
print "Answer:", total

1 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 46 46 accounts for the 1s, then for the tens, then for the hundreds. 46 x 46 x 46, then - 1 because for the first ten, the sum is 45 whereas the rest are 46.

Write each number in the form of a three digit number e.g. $005$ and $019$ We remove the zeros and replace each zero by $1$ since that does not change the product.

Notice $(1+1+2+3+4+5+6+7+8+9)(1+1+2+3+4+5+6+7+8+9)(1+1+2+3+4+5+6+7+8+9)$ have the product of every $3$ digits. But $000$ is not included so subtract $1$ .

Answer = $(1+1+2+3+4+5+6+7+8+9)^{3} -1=46^3-1 = \boxed{97335}$