Product of Digits
Let P ( n ) denotes the product of all nonzero digits of n . Evaluate P ( 1 ) + P ( 2 ) + P ( 3 ) + ⋯ + P ( 9 9 9 ) .
Source : AIME
The answer is 97335.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
I did (1+2+3+4+5+6+7+8+9)=45
3 × 4 5 + 3 × 4 5 2 + 4 5 3 = 9 7 3 3 5
The first term covers the one digit numbers (from 1 to 9) and the "round" tens and hundreds (10, 20, ..., 90 and 100, 200, ..., 900);
the second term is the sum regarding those two digit numbers, which don't have any zero digits and those three digit numbers, which have exactly one zero digit;
and the last term those 3 digit numbers, which don't have a zero digit.
Well done. Me too same way.
I worked out the answer but I couldnt resist to work out for the general case, and the result is beautiful, here it goes
sum |n= 1 to 999 P(n)
can be be written as
sum |n= 1 to 10^3 - 1 P(n)
or in general sum |i = 1 to 10^n - 1 P(i), where n> 0
then, sum |i = 1 to 10^n - 1 P(i) = 45* { sum |j=0 to n-1 (46^j-1) }
or simply
sum |i = 1 to 10^n - 1 P(i) = 45*(1 + 46 + 46^2 + ...... + 46^n-1)
example:
sum |i = 1 to 9 P(i) = 45*(1) = 45
sum |i = 1 to 99 P(i) = 45*(1 + 46^1) = 2115
sum |i = 1 to 999 P(i) = 45*(1 + 46^1 + 46^2) = 97335 (Current Problem)
sum |i = 1 to 9999 P(i) = 45*(1 + 46^1 + 46^2 + 46^3) = 4477455
sum |i = 1 to 99999 P(i) = 45*(1 + 46^1 + 46^2 + 46^3 + 46^4) = 205962975
sum |i = 1 to 999999 P(i) = 45*(1 + 46^1 + 46^2 + 46^3 + 46^4 + 46^5) = 9474296895
.
.
.
sum |i = 1 to 10^n -1 P(i) = 45*(1 + 46^1 + 46^2 + .......46^n-1) - General case
It can also be shown that all sums are mulitples of 9
Brock probably should use the above formula on his program, to save a lot of his computational power, resource and time.
Let S = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 4 5
( 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 ) × ( 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 )
It forms all the possible combinations of the two digit expect the ones with
zeroes .
(
1
×
9
m
e
a
n
s
1
9
a
n
d
9
×
1
m
e
a
n
s
p
r
o
d
u
c
t
o
f
d
i
g
i
t
s
o
f
9
1
)
Now the one with zeroes there are two possible cases that is zero at tens place(single digit integer) or at units place . In both case the sum is S .
So the sum of products for two digit nos is ( S 2 + 2 S ) = 2 1 1 5
For the three digit numbers
( 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 ) × ( 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 ) × ( 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 )
( 9 × 9 × 3 m e a n s p r o d u c t o f d i g i t s o f 9 9 3 )
forms all the possible combinations of the three digit nos expect the ones with
zeroes .
if there is one zero it can come at units place or tens for both the cases
the sum will be S 2 like mentioned above
when there are two zeroes the sum will be S ( c a s e i n c l u d e s 1 0 0 , 2 0 0 . . . . . . . . 9 0 0 ) .
total sum for three digit numbers is S 3 + 2 S 2 + S = 9 5 2 2 0
Therefore the total sum is 2 1 1 5 + 9 5 2 2 0 = 9 7 3 3 5
Python:
1 2 3 4 5 6 7 8 9 10 |
|
Really????? Oh Genius solution indeed!!! Euler would have been proud!!
Log in to reply
Is that sarcasm?
Log in to reply
Oh i didn't know that in any country solving ingenious number theory problems using a computer was considered brilliance. The downvotes for my above quote proves that. BUT That isn't allowed in my country. And i am proud of it.
If u think it otherwise do pay time to your english (THIS IS A JOKE). Ha Ha. Lol.
1 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 46 46 accounts for the 1s, then for the tens, then for the hundreds. 46 x 46 x 46, then - 1 because for the first ten, the sum is 45 whereas the rest are 46.
Write each number in the form of a three digit number e.g. 0 0 5 and 0 1 9 We remove the zeros and replace each zero by 1 since that does not change the product.
Notice ( 1 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 ) ( 1 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 ) ( 1 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 ) have the product of every 3 digits. But 0 0 0 is not included so subtract 1 .
Answer = ( 1 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 ) 3 − 1 = 4 6 3 − 1 = 9 7 3 3 5
Moderator note:
"We remove the zeros and replace each zero by 1 since that does not change the product" should still use a line of explanation for why "the product of non-zero terms is not changed".
The bijection is not expressed in a clear manner for others to understand. You should explain how it is set up / created, while would allow one to follow your argument easily. For example, it is not immediately clear why 000 has appeared, and why "so subtract 1".
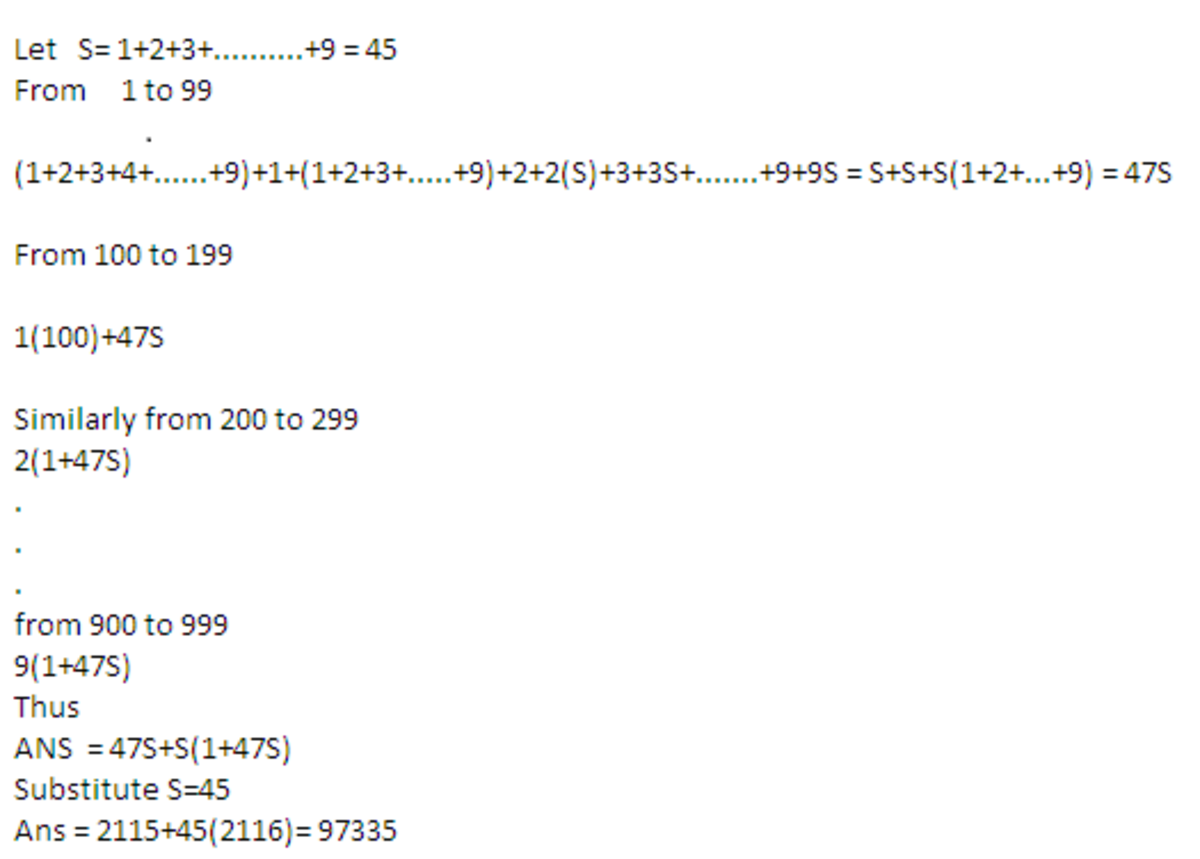
F o r d i g i t s f r o m 1 t o 9 , t h e s u m i s : − 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 N e x t , f o r 1 0 t o 1 9 : − 1 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 T h e n f o r 2 0 t o 2 9 : − 2 ( 1 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 ) A n d s o o n t i l l 9 9 . T h u s , l e t ′ s t a k e S = 1 + 1 + 2 + 3 + 4 + 5 + 6 + 8 + 9 T h u s , f o r d i g i t s t i l l 9 9 w e h a v e . S + S + 2 S + 3 S + 4 S + 5 S + 6 S + 7 S + 8 S + 9 S = 4 6 S N o w f o r 1 0 0 t o 9 9 9 : − 1 × 1 × S + 1 × 2 × S . . . + 1 × 9 × S + 2 × 1 × S + 2 × 2 × S . . . + 9 × 9 × S A d d i n g a l l , w e g e t : − ( 4 6 × 4 6 × S ) − 1 ( B e c a u s e t h e r e ′ s o n e 1 l e s s i n f i r s t i n f i r s t s t e p ) = 4 6 3 − 1 = 9 7 3 3 5