Profiting from predictions

Quantitative Finance Level 2

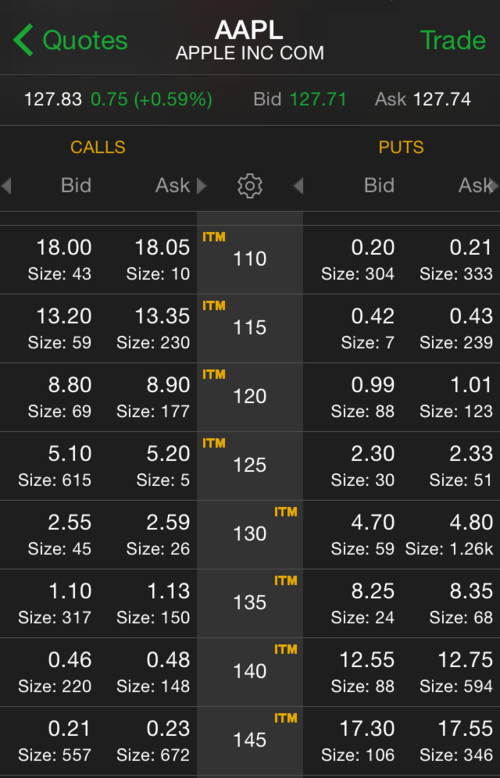Sally expects that APPL stock will rise from its current price of $129.00 to $135.00 on March 20th. Assuming that her prediction comes true , which of the following option strategies would yield the most profit?

Note: No other corresponding trades are done. In particular, she does not hedge her delta exposure.
Ignore interest rate and transaction costs.
There are no dividends.
The image doesn't show the price of options when AAPL is at $129.00.

Image credit: Thinkorswim

Buy the March 20th $130 call Sell the March 20th $125 put Buy the March 20th $125 call Sell the March 20th $130 put Sell the March 20th $135 put Buy the March 20th $135 call

2 solutions

Calvin Lin Staff
Jul 5, 2019

The best trade is selling the $135 put.

Sell $135 put - Made $6 on the intrinsic + Made on the extrinsic at the $135 strike
Buy $125 call - Made $6 on the intrinsic - Lost on the extrinsic at the $125 strike -> Why is this total gain less than selling the $135 put?
Buy $130 call - Made $5 on the intrinsic - Lost on the extrinsic at the $130 strike -> Why is this total gain (most likely) less than buying the $125 call?
Sell $130 put - Made $1 on the intrinsic + Made on the extrinsic at the $130 strike -> Why is this total gain less than selling the $135 put?
Sell $125 put - Made $1 on the intrinsic + Made on the extrinsic at the $130 strike -> Why is this total gain less than selling the $130 put?
Buy $135 call - Made $0 on the intrinsic - Lost on the extrinsic at the $135 strike -> Why is this total gain less than anything else?

Marco Massa
May 8, 2016

Note: This solution is incorrect because it references prices in the image, which are not (completely) reflective of the situation. In particular, the stock last traded at $127.83 with bid-ask of 127.71 at 127.74, which the problem states that the price is $129.

Let's evaluate the P&L for each strategy.

Without referencing the prices in the image, are we able to arrive at the same conclusion?

Calvin Lin Staff - 5 years, 1 month ago

Clearly, the choice should be among

Sell $135 put
Buy $125 call
Buy $130 call

Between the two long positions it is more probable that it is better "Buy $125 Call" otherwise it should be $ask_{125} - ask_{130} > 5$ which is not plausible since the strike prices are near the current stock price.

I think with Put-Call parity relation we can ranking them, but I think we need infomation on the dividends.

Marco Massa - 5 years, 1 month ago

(Assuming no dividends) If we know the expiration price of the stock, we know how much each option will be worth. In this question, the ranked order of outcomes (in terms of return per option, instead of return per $) will be

Sell $135 put - Made $6 on the intrinsic + Made on the extrinsic
Buy $125 call - Made $6 on the intrinsic - Lost on the extrinsic
Buy $130 call - Made $5 on the intrinsic - Lost on the extrinsic (which is more than the $125 call as it's closer to ATM).

Calvin Lin Staff - 5 years, 1 month ago

What subjects can i use to better understand the formulas and equations? if u can help thank ya and greatly appreciate it

Lawrence Webb - 3 years, 4 months ago

Check out the Math for Quantitative Finance course, that guides you to think about these scenarios.

Calvin Lin Staff - 3 years, 4 months ago

So you’re stating the $135 put premium has more value than the difference between the ITM 125 call and the percieved price over 135 at a stock that’s trading @ $129 value? Hmmm, not sure about that. More information is needed in this case , I believe. There are more variables in this situation, I believe.

Ivan Babic - 1 year, 11 months ago

(The solution isn't correct. In particular, the prices cannot be used, since the imag shows a price of 127.83, while the problem states a price of 129.)

More information isn't needed in this case. Hint: The $135 put will be worth $0 on expiry. If you sell it now, what is the minimum price that you can sell it for, and hence what is the minimum that you can profit?
Hint: The $125 call will be worth $10 on expiry. If you buy it now, what is the minimum price that you can buy it for, and hence what is the maximum that you can profit?

Calvin Lin Staff - 1 year, 11 months ago

So the answer would be Sell 135 put as long as the bid - ask remain the same.

Raghav Vedanarayanan - 3 months, 3 weeks ago

Real life scenario: you can only short 1 lot with around 2000$ (in india) as shorting an option requires a huge margin money. But with 2000$ you can buy hell lot of options

SIDDHARTH DHINGRA - 3 months, 1 week ago

Profiting from predictions

Image credit: Thinkorswim

2 solutions

0 pending reports