Is There A Progression of Logs?
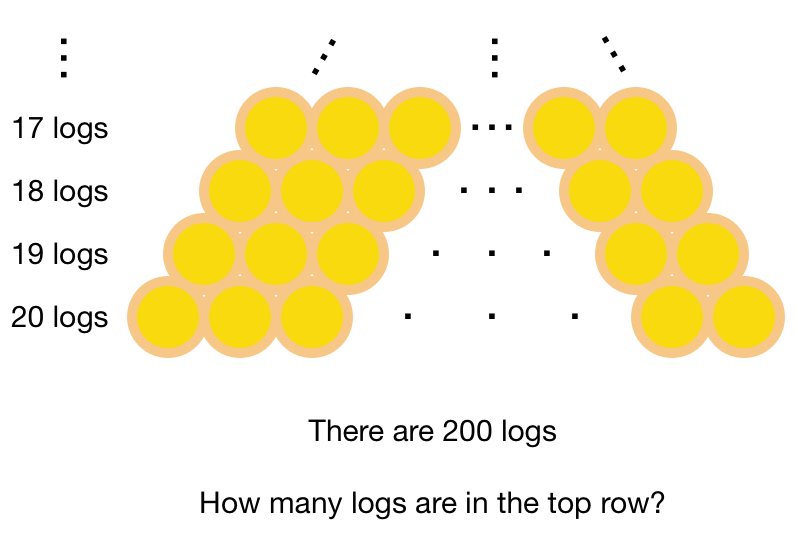
200 logs are stacked in the following manner:
The bottom row has 20 logs,
the row above it has 19 logs,
the row above that has 18 logs,
and so on.
How many logs are there in the top row?
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Gr8 solution (+1) .
Log in to reply
The Question can be done without using any Formula of A.P.
Consider 2 0 0 = 2 0 + 1 9 + 1 8 + ⋯ + l where l is the Last Number
2 0 0 = 2 0 0 + ( − 0 − 1 − 2 − 3 ⋯ − 9 ) + ( 1 0 + 9 + ⋯ + l ) 1 + 2 + 3 + ⋯ + 9 = 1 0 + 9 + ⋯ + l 1 + 2 + 3 + 4 1 0 + 9 + 8 + 7 + 6 + 5 = 1 0 + 9 + ⋯ + l Our Answer l = 5
The 20th triangular number is 20x21 / 2 = 210. That's 10 too many, and 10 is the fourth triangular number, so we remove the first four rows and get our 200, which has the fifth row on top.
Relevant wiki: Arithmetic Progression Sum
Let there be n rows.
Now, using A.P.
2 0 0 = 2 n ( 2 a + ( n − 1 ) d
2 0 0 = 2 n ( 4 0 + 1 − n )
2 0 0 = 2 4 1 n − n 2
4 0 0 = 4 1 n − n 2
n 2 − 4 1 n + 4 0 0 = 0
n 2 − 2 5 n − 1 6 n + 4 0 0 = 0
n ( n − 2 5 ) − 1 6 ( n − 2 5 ) = 0
∴ n = 1 6 , 2 5
n = 2 5 is neglected because rows cannot be more that 20.
a n = a + ( n − 1 ) d
a 1 6 = 2 0 + ( − 1 5 )
a 1 6 = 5
Therefore, 5 logs are there in top row.