Projec-ception
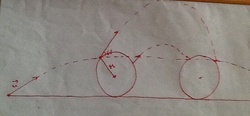 A point mass is projected at an angle
radians from the horizontal. It collides at its maximum height, with a sphere of diameter 72.5 cm. such that it is projected off the sphere, again at an angle
radians from the horizontal. The sphere, due to the collision, is bounced off the floor. The point mass, in its descent, collides with the sphere again, through the same horizontal of the previous point-mass-sphere collision, and is projected at an angle
radians below the horizontal. If the density of the sphere is
kg m
and uniform mass distribution, then the mass of the point-mass is
, and its initial velocity is
. Find
. Assume all the collisions are elastic, and the sphere is rigid.
A point mass is projected at an angle
radians from the horizontal. It collides at its maximum height, with a sphere of diameter 72.5 cm. such that it is projected off the sphere, again at an angle
radians from the horizontal. The sphere, due to the collision, is bounced off the floor. The point mass, in its descent, collides with the sphere again, through the same horizontal of the previous point-mass-sphere collision, and is projected at an angle
radians below the horizontal. If the density of the sphere is
kg m
and uniform mass distribution, then the mass of the point-mass is
, and its initial velocity is
. Find
. Assume all the collisions are elastic, and the sphere is rigid.
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
0 solutions
No explanations have been posted yet. Check back later!