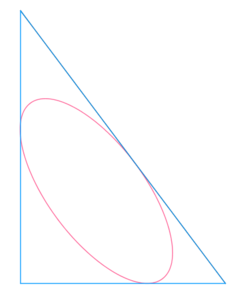
Projected Incircle

Vertices of the triangle are $A(3,0,0)$ , $B(0,4,0)$ and $C(0,0,5)$ . Sides can be easily calculated using Pythagorean theorem: $5, \sqrt{34}, \sqrt{41}$ . The radius of the incircle can be calculated using the formula: $r=\frac{\triangle ABC}{s}$ where s is a semi-perimeter. Area of $\triangle ABC$ can be found using De Gua's theorem: $(\triangle ABC )^2 = ((3 \times 4)^2 + (3 \times 5)^2 + (4 \times 5)^2)/4 \Rightarrow \triangle ABC=\frac{\sqrt{769}}{2}$ The projected incircle is ellipses with major axis $= 2r$ . Minor axis can be obtained by multiplying length of major axis with "the shortening factor". That shortening factor is $1-$ flattening factor of the the ellipse $g$ . It is really cosine of the angle between plane XY and plane a. It is also a ratio of original segment lengths to the projected ones, perpendicular to the intersection line between the two planes.

The shortening factor is of the $\triangle ABC$ can be obtained as $\frac{\triangle ABO } {\triangle ABC}=\frac{3\times 4}{\sqrt{769}}$ where $O$ is the point of origin. The area of the ellipse will be: $\pi r^2 \frac{12}{\sqrt{769}}=6\sqrt{769} π / (\sqrt{34} \sqrt{41} + 5 \sqrt{34} + 5\sqrt{41} + 50)$

$S_{circle}\cos\theta=S_{ellipse}$ , where $\theta$ - is angle between plane $a$ and plane $z=0$ and $\displaystyle \cos\theta = \frac{\frac{1}{5}}{ \sqrt {\frac{1}{3^2}+\frac{1}{4^2}+\frac{1}{5^2}}}$