Projectile at two instants of time
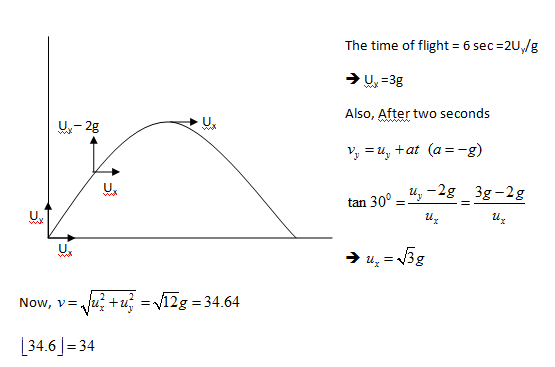
 A projectile thrown from ground moves at an angle of 30 degrees with the horizontal after 2 second of its flight and moves horizontally after further 1 second.
A projectile thrown from ground moves at an angle of 30 degrees with the horizontal after 2 second of its flight and moves horizontally after further 1 second.
Calculate the initial velocity of the Projectile.
Note: Enter the answer as the ⌊ v ⌋ where v is the answer to the problem Take g = 1 0 m / s 2
The answer is 34.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
34.64≈35 , right, sir? Then why the answer is 34?
We didn't fall in dilemma, but some can !
We know Time of Flight (T)
=
g
2
u
sin
x
where
x
is the initial angle of projection.
Here
3
=
g
u
sin
x
,
u
sin
x
=
3
g
After 2 seconds,
velocity in vertical direction =
u
sin
x
−
2
g
velocity in horizontal direction =
u
cos
x
A/q
tan
3
0
=
3
1
=
u
cos
x
u
sin
x
−
2
g
3
1
=
u
cos
x
g
u
cos
x
=
3
g
So,
tan
x
=
3
,
x
=
6
0
u
=
sin
6
0
3
g
=
2
0
3
=
3
4
.
6
4
1
0
1
6
1
5
1
why did you round it into 34 and not 35? It's that sign in the question means "round it down no matter what" or do you own me some points :(( ?
Log in to reply
That sign means greatest integer function
It is box value of velocity not round off velue...
Same is my question......it should be 35....
I think the symbol denotes greatest integer function
What does moves horizontally after further 1 second. mean?
Log in to reply
It means that after (2+1) seconds, the vertical component of velocity becomes 0 and so the motion of the body
at that instant
is
horizontal
.
The time required to do so is half of Time period so I have used
3
=
g
u
∗
s
i
n
x
.
nice shot!!!
1.Using the expression of time of flight over half the range, first find initial velocity along the vertical.
2.Then by using first eqn. of motion, find final velocity along the vertical.
3.Now find final velocity along the horizontal using tan 30=v along y/v along x
4.as motion along horizontal is uniform, initial velocity along horizontal is same as final velocity along horizontal
5.We now have initial velocities along both horizontal and vertical, hence,we can now find the net velocity by taking underoot of squared sum of both of them.We get 34.64 as the answer.
To be clear from the beginning:
-
t = 0, projectile was fired
-
t = 2, projectile is moving at 30 degrees to horizontal
-
t = 3, projectile is horizontal
As g = 10, the vertical velocity will decrease by 10 m/s each second. Thus at t = 2, it must have been 10. At t = 0, it must have been 30.
The only unknown now is the horizontal velocity which is a constant throughout. At t = 2, vertical velocity is 10. Projectile is moving at an angle 30 degrees which means horizontal velocity is 10 x tan(60) = 10 x sqrt(3).
The required answer is then sqrt(300 + 900)
Let the horizontal and vertical components of the initial velocity v be v x and v y = v y ( 0 ) respectively. v x is constant, while v y ( t ) changes with time t .
When the projectile is moving horizontally at t = 3 ⇒ v y ( 3 ) = 0 , and v y ( t ) is given by:
v y ( t ) = v y ( 0 ) − g t ⇒ v y ( 3 ) = v y − 1 0 ( 3 ) = 0 ⇒ v y = 3 0 m / s
At t = 2 ⇒ v y ( 2 ) = 3 0 − 1 0 ( 2 ) = 1 0 m / s
We know that: v x v y ( 2 ) = tan 3 0 ∘ ⇒ v x = tan 3 0 ∘ v y ( 2 ) = 1 0 3 m / s
Therefore,
v = v x 2 + v y 2 = 9 0 0 + 3 0 0 = 1 2 0 0 = 2 0 3 = 3 4 . 6 4 1 0 1 6 1 5 m / s
⇒ ⌊ v ⌋ = 3 4