Projectile Motion Comparison - 3
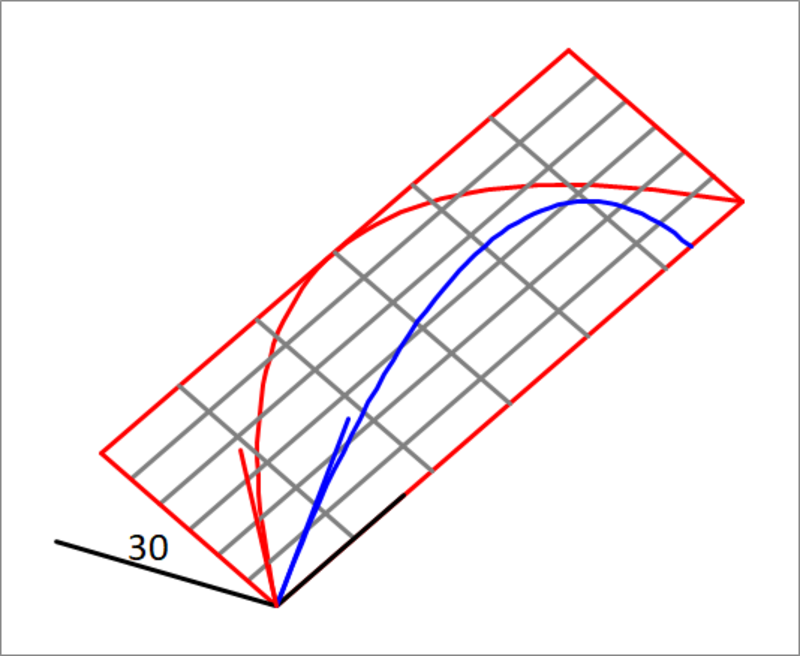
Two solid balls are thrown from the same point with the same linear speed of their centers, the first freely at an angle of 4 5 ∘ with the horizontal, and the second is sent on an inclined plane, with its initial velocity vector making an angle of 4 5 ∘ with the horizontal edge of the plane. The second ball is purely rolling on the inclined plane. How do the ranges of the two balls compare ? The inclined plane makes an angle of 3 0 ∘ with the horizontal ground. If R 1 is the range of the first ball, and R 2 is the range of the second ball, what is the relation between R 1 and R 2 ?
The attached figure depicts the two projectiles. The figure is not drawn to scale.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
First case :
R 1 = g u 2 .
Second case :
Acceleration is 1 4 5 g along the line of greatest slope of the inclined plane.
So, R 2 = 1 4 5 g u 2 = 5 g 1 4 u 2 = 2 . 8 g u 2 .
Therefore R 2 = 2 . 8 R 1 .
Let the speed of projection be u . Consider the second particle to be initially at the origin and it is projected along the plane:
y = 3 x
Gravity is considered to be acting along the − Y direction.
Initial velocity vector:
v o = v o x i ^ + v o y j ^ + v o z k ^
v o = u ( sin 4 5 ∘ cos 3 0 ∘ i ^ + sin 4 5 ∘ sin 3 0 ∘ j ^ + sin 4 5 ∘ k ^ )
This situation is a bit tedious to analyse using Newton's laws with the pure rolling constraint and 3D motion. Instead, here, I apply the Lagrangian approach. Consider the kinetic energy of a pure rolling solid sphere at any instant to be:
T = 1 0 7 m ( x ˙ 2 + y ˙ 2 + z ˙ 2 )
Since y = 3 x :
T = 1 0 7 m ( 4 y ˙ 2 + z ˙ 2 )
The potential energy of the particle is: V = m g y
System Lagrangian: L = T − V
Lagrange's equations read:
d t d ( ∂ y ˙ ∂ L ) − ∂ y ∂ L = 0 d t d ( ∂ z ˙ ∂ L ) − ∂ z ∂ L = 0
y ¨ = − 2 8 5 g z ¨ = 0
Using the constraint equation:
y = 3 x ⟹ y ¨ = 3 x ¨
Therefore:
x ¨ = − 2 8 5 3 g
Solving these three equations gives (Only showing y and z )
y = v o y t − 5 6 5 g t 2 z = v o z t
The Y coordinate of the particle becomes zero at t = 0 and:
t = 5 2 g 2 8 u At this instant, the Z-coordinate is:
z = 1 0 2 8 g u 2 ⟹ R 2 = 2 . 8 R 1