Projectile Motion Comparison
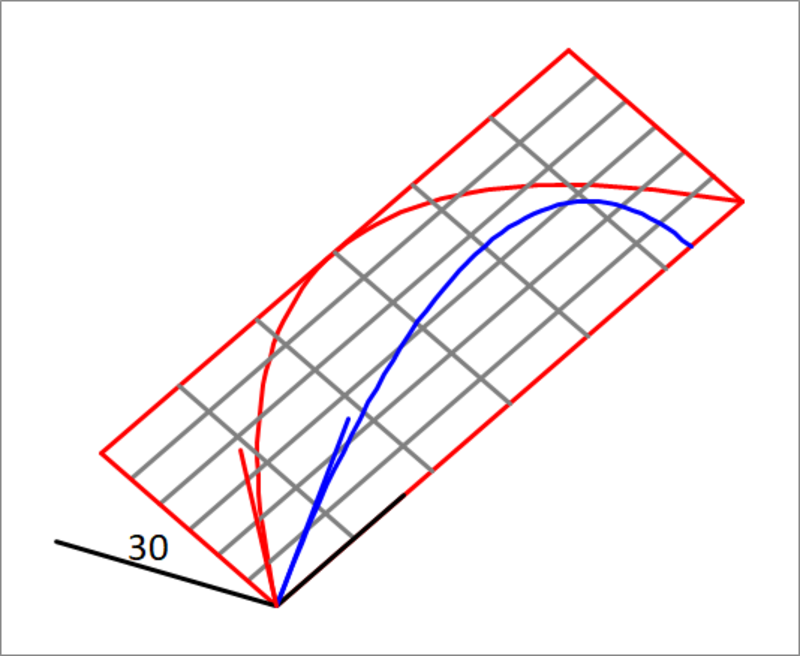
Two balls are thrown from the same point with the same speed, the first freely at an angle of with the horizontal, and the second is sent sliding on an inclined plane, with its initial velocity vector making an angle of with the horizontal edge of the plane. How do the ranges of the two balls compare ? The inclined plane makes an angle of with the horizontal ground. If is the range of the first ball, and is the range of the second ball, what is the relation between and ?
The attached figure depicts the two projectiles. The figure is not drawn to scale.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
This is my attempt at solving the problem rigorously. Let the speed of projection be u . Consider the second particle to be initially at the origin and it is projected along the plane:
y = 3 x
Gravity is considered to be acting along the − Y direction.
Initial velocity vector:
v o = v o x i ^ + v o y j ^ + v o z k ^
v o = u ( sin 4 5 ∘ cos 3 0 ∘ i ^ + sin 4 5 ∘ sin 3 0 ∘ j ^ + sin 4 5 ∘ k ^ )
Now, as the particle slides along the incline, it experiences a normal force due to the plane and gravitational force. Applying Newton's second law gives:
m ⎣ ⎡ x ¨ y ¨ z ¨ ⎦ ⎤ = ⎣ ⎡ 0 − m g 0 ⎦ ⎤ + N ⎣ ⎡ − 0 . 5 3 / 2 0 ⎦ ⎤
Let: 2 m N = P . This simplifies the equations of motion to:
⎣ ⎡ x ¨ y ¨ z ¨ ⎦ ⎤ = ⎣ ⎡ 0 − g 0 ⎦ ⎤ + P ⎣ ⎡ − 1 3 0 ⎦ ⎤
Now consider the constraint equation:
y = 3 x ⟹ y ¨ = 3 x ¨
Using all these equations, eliminating P and re-writing gives the final equations of motion:
x ¨ = 4 − 3 g y ¨ = 4 − g z ¨ = 0
Solving these equations finally yields:
x = v o x t − 8 3 g t 2 y = v o y t − 8 g t 2 z = v o z t
The X and Y coordinates are zero at t = 0 and:
t = g 2 4 u
Plugging this into the Z equation yields the required range:
z = g 2 u 2 R 2 = 2 R 1
Of course, there are easier ways of doing this, but correctly applying the laws of motion helps me understand the nature of the motion, which I completely failed to do so earlier. I look forward to feedback, if necessary. Thanks for sharing this problem.