Projectile on a inclined plane
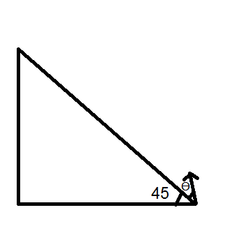 A particle is projected from the bottom of a inclined plane at an angle
with the surface of incline. The incline has an inclination of 1 i.e. angle of incline is 45 degrees. For what value of
will the particle retrace its path after collision with the plane.
A particle is projected from the bottom of a inclined plane at an angle
with the surface of incline. The incline has an inclination of 1 i.e. angle of incline is 45 degrees. For what value of
will the particle retrace its path after collision with the plane.
*Note *
- the collision is an elastic collision.
- the answer is of the form = Find
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let's do this geometrically. So let's take the line x = y and a parabola passing through origin and some point on x axis, whose generic equation is given by y = − k x ( x − a ) where k and a are positive constants. For retrace of the path in elastic collision, the particle must hit the plane normally. That is when x = y the parabola must be having a tangent of slope − 1 . Solve these two and get the slope at origin to be 3. And then we'll get the tan θ = 1 / 2 . Hence the answer 2