Projectile over a Square (part -1)
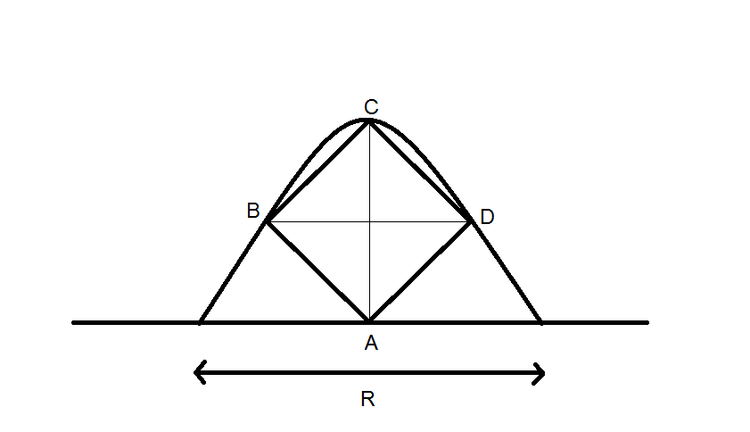 A Square rests on a horizontal plane in such a way that the diagonals of the square are vertical and horizontal. A projectile is thrown from level ground in such a way that the projectile touches all the three vertices which lie in air. If side length of square is
2
0
metres then find the range of the projectile.
A Square rests on a horizontal plane in such a way that the diagonals of the square are vertical and horizontal. A projectile is thrown from level ground in such a way that the projectile touches all the three vertices which lie in air. If side length of square is
2
0
metres then find the range of the projectile.
The answer is 40.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I believe there's a typo in your solution. It should be AD instead of OD.
This problem is more geometry than mechanics. Since the path of the projectile is a parabola its equation taking the origin A midpoint of R due symmetry will be of the form
x 2 = a ( d − y )
we must determine the constants a and d.
For x= 0 ; y= d ; being d the diagonal of the square and for x=d/2 ; y=d/2 we get constant a=d/2.
Then we get
x
2
=
d
/
2
(
d
−
y
)
so R values two times x when y=0 .
Then R = d 2 ... and since d = 2 0 2 ... we get R = 4 0 meters
It is easy to tell that the equation of the trajectory is − 1 0 2 ( y − 2 0 2 ) = x 2 and since we want to find the range, y = 0
Making y the equation of the trajectory gives:
− 1 0 2 x 2 − 4 0 0 = y
Solving − 1 0 2 x 2 − 4 0 0 = 0 gives
x = 2 0 o r − 2 0
Therefore, the answer is 2 0 − ( − 2 0 ) = 4 0
Since the horizontal velocity of a projectile is constant. Its horizontal displacement is directly proportional to time (\t) of travel.
Let center of the square be O , the end of the projectory on the horizontal plane be E , the time taken for the projectile to travel from C to D be t 1 and from C to E be \(t_2). Then, we have:
\(\dfrac {1}{2}gt_1^2= 10\sqrt{2}\quad \quad \dfrac {1}{2}gt_2^2= 20\sqrt{2}\quad \Rightarrow \dfrac {t_2^2}{t_1^2} = 2\quad \Rightarrow \dfrac {t_2}{t_1} = \sqrt{2}\)
⇒ O D A E = t 1 t 2 = 2 ⇒ A E = 2 O D = 2 0 m
Therefore, R = 2 × A E = 4 0 m .