Projectile over a Square (part -2)
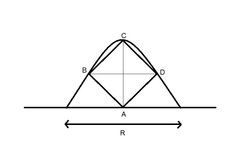 A Square rests on a horizontal plane in such a way that the diagonals of the square are vertical and horizontal. A projectile is thrown from level ground in such a way that the projectile touches all the three vertices which lie in air. If side length of square is
2
0
metres then find the angle of projection.
A Square rests on a horizontal plane in such a way that the diagonals of the square are vertical and horizontal. A projectile is thrown from level ground in such a way that the projectile touches all the three vertices which lie in air. If side length of square is
2
0
metres then find the angle of projection.
Note: The angle of projection is of the form
θ
=
t
a
n
−
1
a
b
Find a + b
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
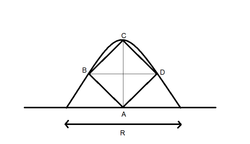 Let AC be the y-axis and the horizontal be the x-axis. It can easily be seen that the equation of parabola passing through points B,D and C is
−
1
0
2
(
y
−
2
0
2
)
=
x
2
by basic transformations of
y
=
x
2
. Find the slope of this by differentiating with respect to x at x=-20; we get
d
x
d
y
x
=
−
2
0
=
1
0
2
−
2
x
=
2
2
. Hence the answer
4
Let AC be the y-axis and the horizontal be the x-axis. It can easily be seen that the equation of parabola passing through points B,D and C is
−
1
0
2
(
y
−
2
0
2
)
=
x
2
by basic transformations of
y
=
x
2
. Find the slope of this by differentiating with respect to x at x=-20; we get
d
x
d
y
x
=
−
2
0
=
1
0
2
−
2
x
=
2
2
. Hence the answer
4
well this was really interesting by making the question simpler by coordinate geometry. i did this by first applying Max height formula and obtained the vertical component of the initial velocity. then applying equation of motion in y direction for height 10sqrt(2) , then obtained the difference of roots of the quadratic in time t ...then horizontal component of velocity multiplied by the difference of roots equating to 20sqrt(2) then i divided to get tan of the angle projected as 2sqrt(2)
pl explain this equaion of parabola
Can we have a solution with some physics in it
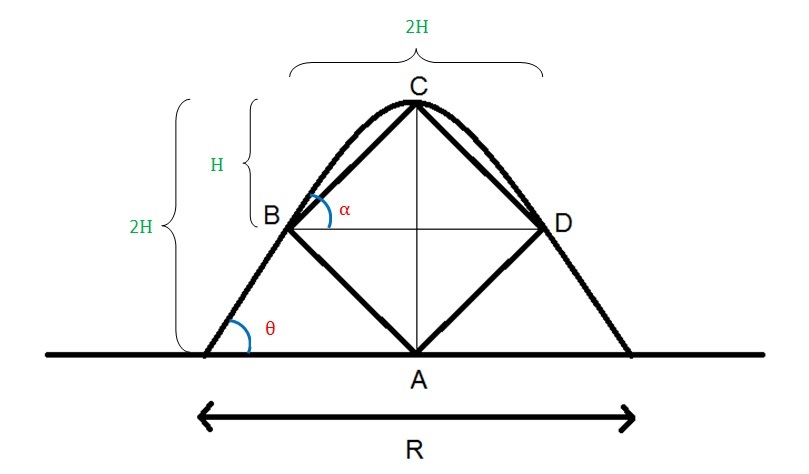
Let velocity of the particle at the time of projection be u & at point B be v .
First let concentrate on part BCD of the Projectile. It can also be called as a projectile with initial velocity u , at an angle α from horizontal, H m a x = H & Range ( R 1 ) = 2 H .
So, t a n α = R 1 4 H m a x = 2
And H = 2 g u 2 s i n 2 α
⟹ u s i n α = 2 g H
⟹ u c o s α = 2 g H × c o t α
or, u c o s α = 2 g H .
Now come to the projectile from ground.
2 g v 2 s i n 2 θ = 2 H
⟹ v s i n α = 4 g H
⟹ v c o s θ = 4 g h × c o t θ .
Since v c o s θ = u c o s α so 4 g h × c o t θ = 2 g H .
Therefore t a n θ = 2 2
Hence the answer is 2 + 2 = 4 .