Projectile Puzzle
The maximum horizontal distance you can throw an object before it hits the ground is given by , where is a constant and is the maximum height the object reaches if thrown directly upwards at the same initial speed.
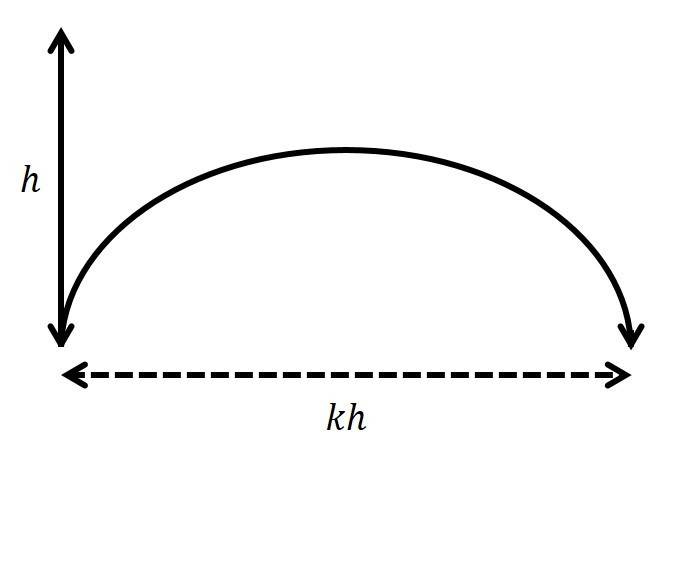
What is the value of ?
Details and Assumptions
-
There is no air resistance.
-
The object is thrown from ground level in both cases.
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Firstly, recall that, at its highest point, the object thrown upwards will have a GPE equal to it initial KE.
m g h = 2 1 m v 2
g h = 2 1 v 2
v = 2 g h
As stipulated in the question, the object thrown for maximum horizontal distance also has this initial speed.
In order to get it to go as far as possible before hitting the ground, the angle at which it is projected must be 4 5 ° . This yields the following:
Using this, we can work out the time of flight. The vertical component of the object's velociy is sin 4 5 × 2 g h , and this can be substituted into the SUVAT equation v = u + a t :
u = sin 4 5 × 2 g h
v = 0
a = − g
t = ?
0 = sin 4 5 × 2 g h − g t
t = − g − sin 4 5 × 2 g h
This is the time taken to reach the highest point during the object's flight; the total flight time will be double this:
2 × g sin 4 5 × 2 g h
Now it is simply the the case of using the familiar s = v t equation with the horizontal component of the object's velocity (which is constant) to find the total horizontal distance travelled when the object hits the ground:
( 2 × g sin 4 5 × 2 g h ) × ( cos 4 5 × 2 g h )
= ( 2 g h ) 2 × cos 4 5 × sin 4 5 × 2 ÷ g
= 2 g h ÷ g × 0 . 5 × 2
= 2 h
Thus, the object's largest horizontal distance is double its maximum height; the solution is 2 .