Projectiles aren't as easy as you might think
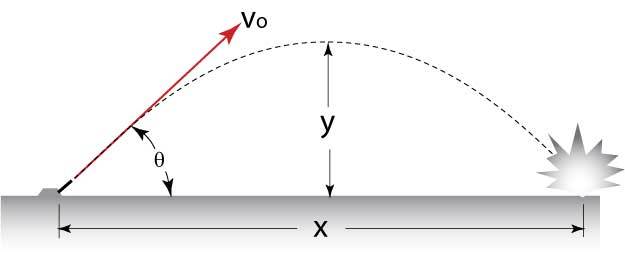 A ball is thrown from ground With a velocity
, and at an angle
. With what angle
should the ball be thrown to give it maximum arc length or maximum distance for its trajectory to cover? If
is the maximum value find:
A ball is thrown from ground With a velocity
, and at an angle
. With what angle
should the ball be thrown to give it maximum arc length or maximum distance for its trajectory to cover? If
is the maximum value find:
in degree?
Details and Assumptions
Maximum range doesn't necessarily mean maximum arc length.
The answer is 56.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Link