Projectiling?

Classical Mechanics Level 3

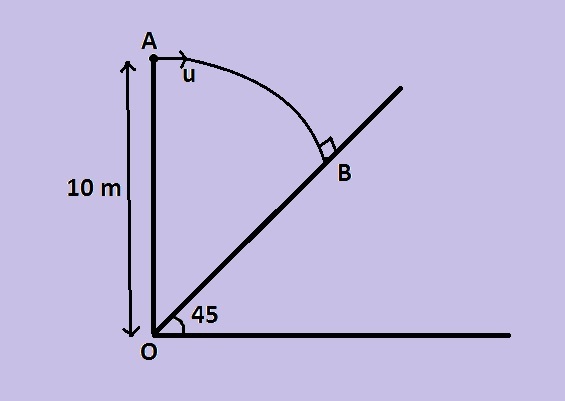
A particle is projected horizontally with speed u u from a point A which is 10 m 10 m above the ground. If particle hits the inclined plane perpendicularly at point B. ( g = 10 m s − 1 ) g=10 ms^{-1})

Q1. Find the horizontal speed with which the particle was projected.

Q2. Find the length OB along the inclined plane.

Q3. Find the speed at point B.

10 3 2 , 20 2 3 , 10 3 10\sqrt{\frac{3}{2}}, \frac{20\sqrt{2}}{3}, \frac{10}{\sqrt{3}} 10 2 3 , 20 2 3 , 20 3 10\sqrt{\frac{2}{3}}, \frac{20\sqrt{2}}{3}, \frac{20}{\sqrt{3}} 20 20 3 , 20 3 , 10 3 20\sqrt{\frac{20}{3}}, 20\sqrt{3}, 10\sqrt{3} 20 3 , 10 3 , 20 3 \frac{20}{3}, \frac{10}{\sqrt{3}}, \frac{20}{\sqrt{3}}

Rishabh Tripathi by Rishabh Tripathi , 22, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Ahmed Hossain
Nov 23, 2016

1=(gt)/u; gt=u; again; 10-.5gt^2=ut; 10-.5gt^2=gt^2; (3/2)gt^2=10; t^2=(2*10)/(3g); t=(2/3)^.5; u=10(2/3)^.5; hence the answer is the last option

6 Helpful 0 Interesting 0 Brilliant 2 Confused

Agr aap ans.upload kr rhe Ho Toh easy language me kiijiye na.. At least samj to aaye

Devesh Saraswat - 2 years, 10 months ago

Please explain the 2nd and 3rd part of the question properly very fat. .....please

Sai Pallavi - 2 years, 10 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...