Proof Without Words

Algebra Level 1

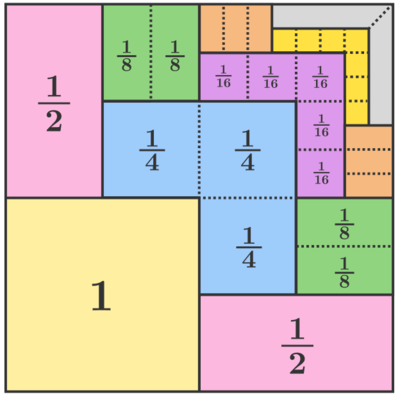
What algebraic identity is this?

1 + \frac{2}{2} + \frac{3}{4} + \frac{4}{8} + \frac{5}{16} + \cdots = 4

1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \cdots = 2

1 + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots = \frac{ \pi^2}{6}

1 + \frac{1}{2} + \frac{1}{3} + \frac{ 1}{4} + \frac{1}{5} + \cdots = \infty

3 solutions

Michael Mendrin
Jan 24, 2017

The figure suggests that it's a $2$ x $2$ square with an area of $4$ . Assuming this, we can see how there's $1$ tile with an area of $1$ , $2$ tiles each with an area of $\frac{1}{2}$ , $3$ tiles each with an area of $\frac {1}{4}$ , etc. These comments have been added otherwise Brilliant.org sends the solution back "for more and better explanation".

It's a great picture, though I don't think I would call it a "Proof Without Words".

Peter Byers - 4 years, 4 months ago

Do you need an explanation with this one too? Proof Without Words-Part 6

Michael Mendrin - 4 years, 4 months ago

dirty proof

pms shashank - 4 years, 4 months ago

no, not a dirty proof. It's a clean proof. As clean as proofs go.

Michael Mendrin - 4 years, 4 months ago

Chandresh Chouhan
Jan 27, 2017

Let S=1+2(1/2)+3(1/4)+4(1/8)+.............
and
S1=1+1/2+1/4+1/8+1/16+...........
and
S2=1/2+2(1/4)+3(1/8)+4(1/16)+..........
since S1+S2=S
and S2=1/2+2(1/4)+3(1/8)+4(1/16)+..........=1/2[1+2(1/2)+3(1/4)+4(1/8)+.............]=1/2(S)
Therefore, S1+S2=S implies, S=2*S1=2[1+1/2+1/4+1/8+1/16+...........]=2[1/(1-1/2)]=4
and pictorially, 4x1=4.
Hence Proved.

Md,shafiqul Alom
May 20, 2017

Since one forth of total area=1,so the total area=4*1=4 though we can calculate many interesting ways.

Proof Without Words

3 solutions

0 pending reports