Proof Without Words — Part 5

Algebra Level 3

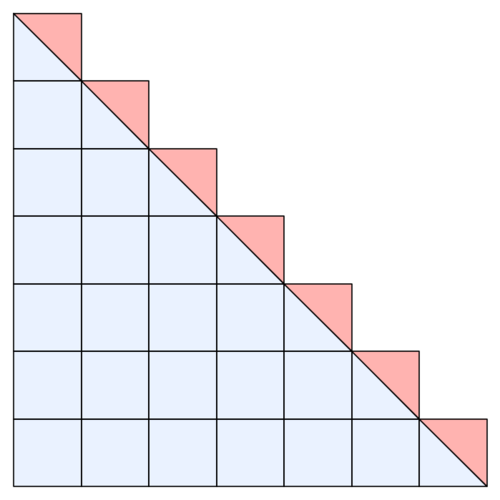The picture above illustrates which of the following:

1 + 3 + 5 + \dots + (2n-1) = n^2

a^2 + b^2 = c^2

1 + 2 + 3 + \dots + n = \frac{n^2}{2} + \frac{n}{2}

1 + 2 + \dots + n + \dots + 2 + 1 = n^2

8 solutions

Eswarlal B Krishnamoorthy
Mar 14, 2014

The squares should be added diagonally from the left bottom. It is 1+2+3+4+5+.........+n=n(n+1)/2.

lol; i understand; but the first time i saw it; i rush to answer a^2+b^2=c^2 then suddenly its not a^2+b^2=c^2. but it is true if we are going to look at the hypotenuse of the big triangle which is the length of the diagonal of the square at the top. The question is why it had been emphasize by the color there; I guess the color is misleading; it will lead us to choose the pythagorean theorem

Erickson Fajiculay - 7 years, 2 months ago

I made the same error for the same reason. Bad diagram, IMHO.

Don Weingarten - 2 years, 4 months ago

Did not get it!

Yash Gada - 7 years, 2 months ago

consider each unit as value 1
So area of one box is 1 and when we add up area of each row from top to bottom it is 1+2+3...+n
Now the blue shaded region is half of the square having side n. Area of blue shaded region is n^{2} / 2
Then area of one red triangle is 1/2 * 1 *1 (1/2 * b * h) which is 1/2
Area of n triangle n/2
add up we get n^{2} / 2 + n/2

Saran Prasath - 7 years, 2 months ago

from the top, start line by line counting, at the end of Nth line, no. of squares are =n(n+1)/2

Manish Jha - 7 years, 3 months ago

I thought that it was a^2 +b^2=c^2

Aman Jaiswal - 7 years, 2 months ago

I did not understand.

Ninad Akolekar - 7 years, 3 months ago

how is it ? explain please

Aadharshini Madhanagopal - 7 years, 2 months ago

why it can't be a^2 +b^2 = c^2

Mohit Tripathi - 7 years, 2 months ago

consider each unit as value 1
So area of one box is 1 and when we add up area of each row from top to bottom it is 1+2+3...+n
Now the blue shaded region is half of the square having side n. Area of blue shaded region is n^{2} / 2
Then area of one red triangle is 1/2 * 1 *1 (1/2 * b * h) which is 1/2
Area of n triangle n/2
add up we get n^{2} / 2 + n/2

Saran Prasath - 7 years, 2 months ago

Great !!!

Tanmay Meher - 7 years, 2 months ago

explain how to solve it...

Rahul Sharma - 6 years, 11 months ago

It's more of a pythagorean relation

Chris Claron - 6 years, 11 months ago

if u see every white box as a combo of two white triangles; and every red triangle as the subtracted one then we can better look at the series third that fits the most as follows...

1 + 2 + 3 + ······· + n =  (n² + n)/2

2( 1 + 2 + 3 + ······ + n) =  n² + n

2( 1 + 2 + 3 + ······ + n) – n   =  n²

Rohit Kumar - 3 years, 11 months ago

Tùng Michael
Mar 15, 2014

Set the area of 1 small square = 1. We have In the 1st line: 1 square In the 2nd line: 2 squares ..... In the "nth" line: n squares => the area of blue big triangle is: (the area of all small squares in all lines = 1+2+3+...+n ) - (the area of pink triangles= n/2) on the other hand we can calculate the area of blue big triangle by "normal" way, which is: n.n/2 So: (1+2+3+...+n) - n/2 = (n^2)/2 => done

yeah...that correct explanation

Max B - 7 years, 2 months ago

Karim Massi
Apr 3, 2014

THE number of half triangle precise the number of square in the big triangle so 1+2+3+... = n(n+ 1)/2

Amanda Hm
Mar 29, 2014

The squares show 1+2+3+...n from right to left The green part shows: n^2/2 The red parts show: n/2

Phil Blair
Mar 20, 2014

1/2 a square of side n is n**2/2. Add n/2 to pick up the n pink triangles.

Rekha Rani
Mar 16, 2014

the squares are in the form of 1+2+3+4.....+(n-1)+n=n(n+1)/2 the squares are 7 in the bottom row . place 7 in n(n+1)/2.
we will get answer= 7(7+1)/2=28
count no of squares in the fig we will get 28 squares.

Sunil Pradhan
Mar 16, 2014

to find total number of squares in the figure 1 + 2 + 3 + ... + n = n(n+1)/2

= n²/2 + n/2

Badagha Jivan
Mar 16, 2014

The squares should be added diagonally from the left bottom. It is 1+2+3+4+5+.........+n=n(n+1)/2.

Proof Without Words — Part 5

8 solutions

= n²/2 + n/2

0 pending reports