Proof Without Words – Part 6

Algebra Level 4

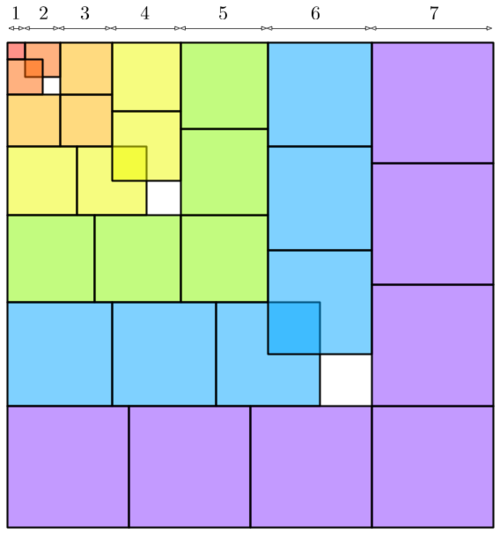The image above illustrates which of the following identities?

1^3 + 2^3 + 3^3 + \dots + n^3 = \frac{1}{4}\left[n(n+1)\right]^2

1 + 3 + 5 + \dots + (2n-1) = n^2

1^2 + 2^2 + 3^2 + \dots + n^2 = \frac{n(n+1)(2n+1)}{6}

1^3 + 2^3 + 3^3 + \dots + n^3 = (1 + 2 + 3 + \dots + n)^2

2 solutions

Milly Choochoo
Mar 20, 2014

You can sort of get the idea of the picture by looking at, for example, the $(1+2+3)^2$ square. Upon inspection (mentally making a grid of $1 \times 1$ squares out of the picture), you can see that the hole next to the $2 \times 2$ square has an area of one unit/grid-cell, which is the same area as the square made by the overlapping of the $2 \times 2$ squares. In fact, all of the holes/blank spots have the same area as the overlapping square to their top-left . This means that you can say the area of that $(1+2+3)^2$ square is $(1+(2\times 2^2) + (3\times 3^2))$ .

By multiplying through, you can then generalize this to $1^3 + 2^3 + \ldots n^3 = (1 + 2 + \ldots n)^2$ .

I think there were 2 correct alternatives for this question, because ${ (1+2+3+...+n) }^{ 2 }={ \left( \frac { n(n+1) }{ 2 } \right) }^{ 2 }=\frac { 1 }{ 4 } { \left[ n(n+1) \right] }^{ 2 }$

Eloy Machado - 7 years, 2 months ago

You stated a true identity, but that is not reflected in the diagram. There is no indication of why

$1 + 2 + 3 + \ldots + n = \frac{ n(n+1) } { 2}$ .

Hence, the other identity is not illustrated in the image.

Calvin Lin Staff - 7 years, 2 months ago

Oh, I see. Thank you.

Eloy Machado - 7 years, 2 months ago

Yes Calvin. Thank you.

The purpose is not to state which of these equations is correct. All of them are correct. The purpose is to state which of the equations given is represented/illustrated by the diagram.

Milly Choochoo - 7 years, 2 months ago

But I Solved It Easily By Looking At block (1+2) and (1+2+3) block and I Found It....

Anand Raj - 7 years, 1 month ago

you are wrong

Anuj Shikarkhane - 7 years ago

(1+2+3......)=( n(n+1))/2

Vamshidhar Reddy - 7 years, 2 months ago

(1^3 + 2^3 +3^3.......n^3)=(n(n+1)/2)^2

Adhithya Raghav - 7 years, 2 months ago

We are just waiting for part 7.

Gaurav singh - 7 years, 1 month ago

yes....both option 1 and option 4 are correct........i didnt clicked wrong

Navneet Mundhra - 7 years, 1 month ago

Shree Lakshmi
Mar 24, 2014

from the image we can infer that square of 1 is repeated 1 time, square of 2 is repeated 2 times and so on up to n. This gives the sum of cubes of first n integers.But the area of the complete square is the square of sum of first n integers. Equating both gives us the required answer.

Proof Without Words – Part 6

2 solutions

0 pending reports