We Thought This Was Hard, Till We Saw This Image.
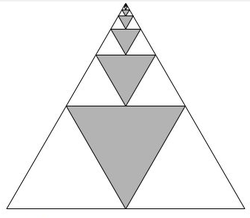 Consider the above image of equilateral triangles, where those that point down are shaded grey and those that point up are shaded white. Which of the following properties does it demonstrate?
Consider the above image of equilateral triangles, where those that point down are shaded grey and those that point up are shaded white. Which of the following properties does it demonstrate?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
why not the first option?
Log in to reply
though parallel lines..but the spacing between lines decreasing..become infinitely small.tends to zero..again for a paralell lines..they can meet at infinity
Log in to reply
+Arunima Mor Yes parallel lines dont meet at infinity also in this case they will simply over overlap if you are saying that at infinity the distance between them will be zero as it keeps on becoming smaller. Yet they are just overlappping and are yet parallel. So i think that could be the answer too
There's a far quicker way of showing that the area shaded grey (that's "gray" for those in the US) is 1/3 which is to consider the shape as a series of trapeziums (trapezoids).
The largeet is formed by the three equialateral triangles at the bottom of the original one (two white ones pointed upwards, and a grey one that's inverted). One third of this trapezium is grey. Now ignore those three triangles and conser the remaining one in exactly the same way.
It's a nice iterative approach that has a certain visual appeal. And yes, I am aware that wasn't what the question asked!
how van you say that the area of the biggest shaded triangle is 1/4 of the whole?
So, when you look at the picture, the first gray region is 1/4 of the overall, the second 1/4 of 1/4 of the triangle, and so on... Let's make an equation for the area of the gray: x=1/4+1/16+1/64.... 4x=1+1/4+1/16... If you subtract the two equations, you get: 3x=1, so x=1/3, so the answer is D.
How does the image itself demonstrate this property? All of the options are true statements, so what makes this the answer?
Log in to reply
Hey Calvin, can you pls. tell me how to submit my question to brilliant staff? I post the question but it neither carries the difficulty level tag nor is it shared to many people. I have waited for weeks for my question's turn to come but nothing happens. Please help me. I would be obliged.
it's corrct
Every time we are dividing the triangle in four equal part, and we are leaving three parts and considering only one for further division.
So, after first step.
( part already divided ) + ( part to be divided ) = area of triangle.
3 * 1/4 + 1/4 =1
2nd step
3 * 1/4 + 1/4( 3/4 +1/4) =1
3rd step
3 * 1/4 + 3 * 1/4^2 +1/4 ^2 ( 3/4 +1/4 ) =1
after n steps
3 * 1/4 + 3 * 1/4^2 + .... ... +3 * 1/4^n +1/4 ^n ( 3/4 +1/4 ) =1
so after infinite steps ( right most term of left side will become zero after infinite steps. )
3 * 1/4 +3 * 1/4^2 + 3 * 1/4^3 +3 * 1/4^4 + 3 * 1/4^5 + .... ... .... ... =1
so 1/4 +1/4^2 + 1/4^3 +1/4^4 + 1/4^5 + .... ... .... ... = 1/3
nice try but too confusing!!!!
eassy the first gray region is 1/4 of the overall, the second 1/4 of 1/4 of the triangle, and so on... Let's make an equation for the area of the gray: x=1/4+1/16+1/64.... 4x=1+1/4+1/16... If you subtract the two equations, you get: 3x=1, so x=1/3,
Great Answer.
Each time, the area of the shaded region is 1/4 of the area of the triangle it was previously a part of. Extending this to an infinity sequence, where the process of dividing the triangle continues, we get the areas 1/4, 1/16, 1/64, and so on. And the sum of this Geometric Progression is 1/4 * (1- 0)/ (1-1/4) => 1/3 From the figure, we can see that in each 'level/step' of the triangle (so to speak), it is clear that 1/3 of the area in each trapezoidal level is shaded. That is, we can infer that the area of the triangle is the sum of the areas of these steps. And since 1/3 of each step is shaded, we can conclude that the areas of these shaded triangles must equal 1/3 of the area of the triangle. This image therefore gives a conclusive proof of the formula we used above to calculate the sum of the infinite GP.
sum of area of all triangles (gray & white) inside equilateral triangle(side=a)=((3/16)^(1/2)) a^2,,and this method leads to option as follow.. 3 (3/16)^(1/2) (a/2)^2 + 3 (3/16)^(1/2) (a/4)^2 + 3 (3/16)^(1/2) (a/8)^2 +.........=((3/16)^(1/2)) a^2 => (1/4)+(1/4)^2 +(1/4)^3 +..........=(1/3)
first consider the lower three triangles which is 3/4 and the shaded part is 1/4, And if you go similarly divide the upper triangle 1/4 into again four parts. and recursively consider the below three parts, 3/16 and the shaded part is 1/16, so here for every set of three triangles right from below one part is shaded and other two are unshaded. Hence if we go on doing this infinitely we will end up in shading one third of the entire triangle. So summing up all the shaded triangles 1/4+1/16+1/64+....... will lead to 1/3.
First,notice that the largest triangle can be divided into small triangles so that the total area can be divided into small areas, hence; the total area equal 3 times the area of the largest shaded triangle plus 3 times the area of the second-largest triangle plus 3 the area of .... and so on . And if we calculate the area of every single shaded triangle it will be (sqrt(3)/4)(Xn)2 .. X is the length of the rib of triangle number n .. then we get the sum of the area of every shaded triangle and multiply it by 3 .. This will give the total area as shown in the paper ( First equation ) .. then if we let the length of the rib of the largest shaded triangle =X ,the length of the smaller triangle's ribs =X/2 and so on ..Also the length of the rib of the largest triangle = 2X.. So when we substitute in the first equation we will get the formula of the first choice ..
First, notice that the are of the largest shaded triangle is 4 1 of the original triangle.
The area of the second-largest shaded triangle is 4 1 × 4 1 = 4 2 1 of the original triangle.
The third-largest one will be 4 3 1 , and so on.
So, the total area of the shaded triangles is 4 1 + 4 2 1 + 4 3 1 + … of the original triangle's area.
Now, look at the three triangles located in the lowest part of the figure. Notice that one out of the three triangles is shaded.
Looking at the next three triangles above them also tells us that one out of those three triangles is shaded.
The pattern goes on, and so, we can conclude that the shaded triangles' total area is exactly 3 1 of the original triangle's area.
Basically, the two boxed expressions above is equal, because they state the area of the shaded triangles, compared to the original triangle. Hence, it's proved that
4 1 + 4 2 1 + 4 3 1 + … = 3 1