Proof Without Words

Algebra Level 3

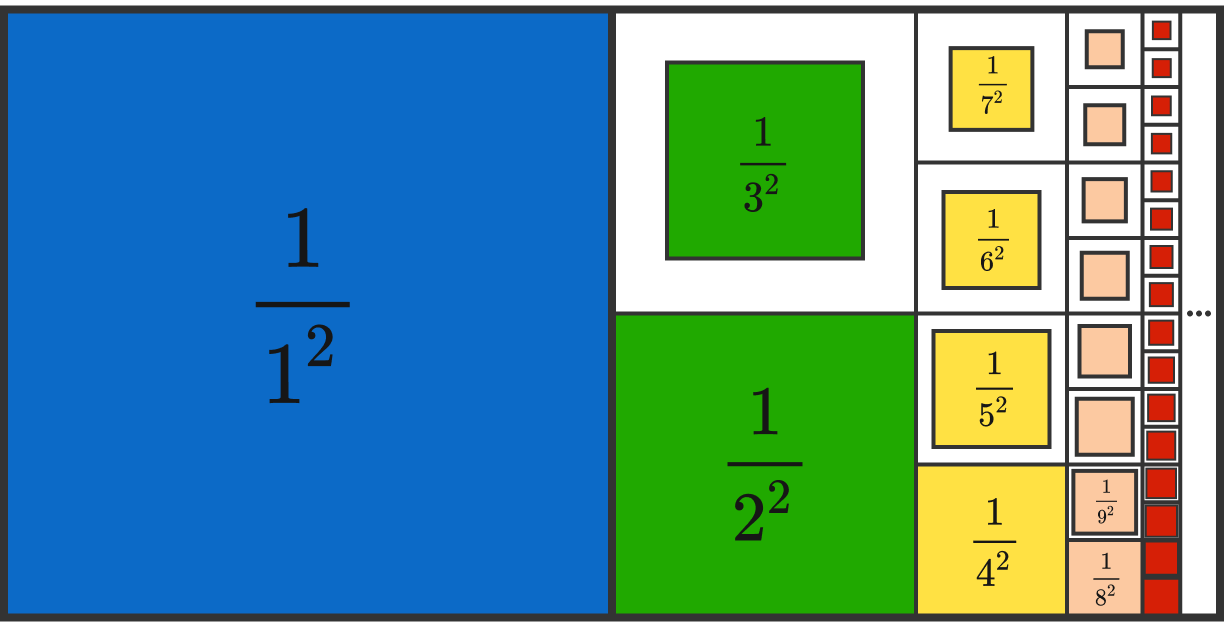
What mathematical fact is demonstrated above?

∑ n = 1 ∞ 1 2 n = 2 \sum_{n=1}^\infty \frac{1}{2^n} = 2 ∑ n = 1 ∞ 1 n < 2 \sum_{n=1}^\infty \frac{1}{n} < 2 ∑ n = 1 ∞ 1 n 2 = π 2 6 \sum_{n=1}^\infty \frac{1}{n^2} = \frac{\pi^2}{6} ∑ n = 1 ∞ 1 n 2 < 2 \sum_{n=1}^\infty \frac{1}{n^2} < 2

Calvin Lin by Calvin Lin

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Tom Van Lier
Feb 6, 2017

The big blue square has half the area of the rectangle => the area of the rectangle is 2.

The area of the squares gets smaller according to a series determined by 1 n 2 \frac{1}{n^2} .

All these squares fit together into the big rectangle.

=> The sum of these areas is smaller than 2, the series converges to something smaller than 2

13 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

How do we know that the big blue square has half the area of the rectangle?
We're using the fact that 1 2 0 + 1 2 1 + 1 2 2 + 1 2 3 + … = 2 \frac{1}{2^0} + \frac{1}{2^1} + \frac{1}{2^2} + \frac{1}{2^3} + \ldots = 2 .

That is indeed an interesting observation. It turns out that ∑ 1 n \sum \frac{1}{n} is, however, divergent. This means no matter how large a real number you choose, you cannot bound the sum with it.

Agnishom Chattopadhyay - 4 years, 4 months ago

This is a really neat way of proving that the sum of reciprocal of squares is a convergent sequence mainly because it uses simple geometry concepts like area of squares.

In fact, the sum converges to π 2 6 \dfrac{\pi^2}{6} which is about 1.644... Can we find a tighter upper bound (or find the actual convergent value) by using geometry?

Pranshu Gaba - 4 years, 4 months ago

Log in to reply

I don't know how to find a tighter upper bound using geometry, but I did manage to show that the upper bound can be reduced in a systematic manner. Take a look below!

∑ j = 1 ∞ 1 j 2 = 1 + 1 2 2 + ∑ j = 3 ∞ j j 3 < 5 4 + ∑ j = 3 ∞ j ( j − 1 ) j ( j + 1 ) = 5 4 + ∑ j = 3 ∞ 1 ( j − 1 ) ( j + 1 ) = 5 4 + 5 12 = 5 3 \sum_{j=1}^\infty \dfrac1{j^2} =1 + \dfrac1{2^2} + \sum_{j=3}^\infty \dfrac{j}{j^3} < \dfrac54 + \sum_{j=3}^\infty \dfrac j{(j-1)j(j+1)} = \dfrac54 +\sum_{j=3}^\infty \dfrac 1{(j-1)(j+1)} = \dfrac54 + \dfrac5{12} = \dfrac53

with the final series represents a telescoping series .

Surely, we can improve on this even further, right?

Pi Han Goh - 4 years, 4 months ago

Log in to reply

Very nice reduction. 5 3 = 1.666 \frac{5}{3} = 1.666 which is very close to π 2 6 \frac{ \pi^2 } { 6} , so I think any further improvement will take a lot of work.

Of course, we could pull out an additional term before doing the partial fraction summation (but that to me doesn't constitute a different approach).

Calvin Lin Staff - 4 years, 3 months ago

Well that is why I saw it as a 'demonstration', more than a proof. Because if you look at it in a different way, you may use this argument to intuitively demonstrate the correct answer. I know that is not a proof, but that is not how I interpreted 'demonstrated' .

Tom Van Lier - 4 years, 3 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...