Properly Ranking Teams
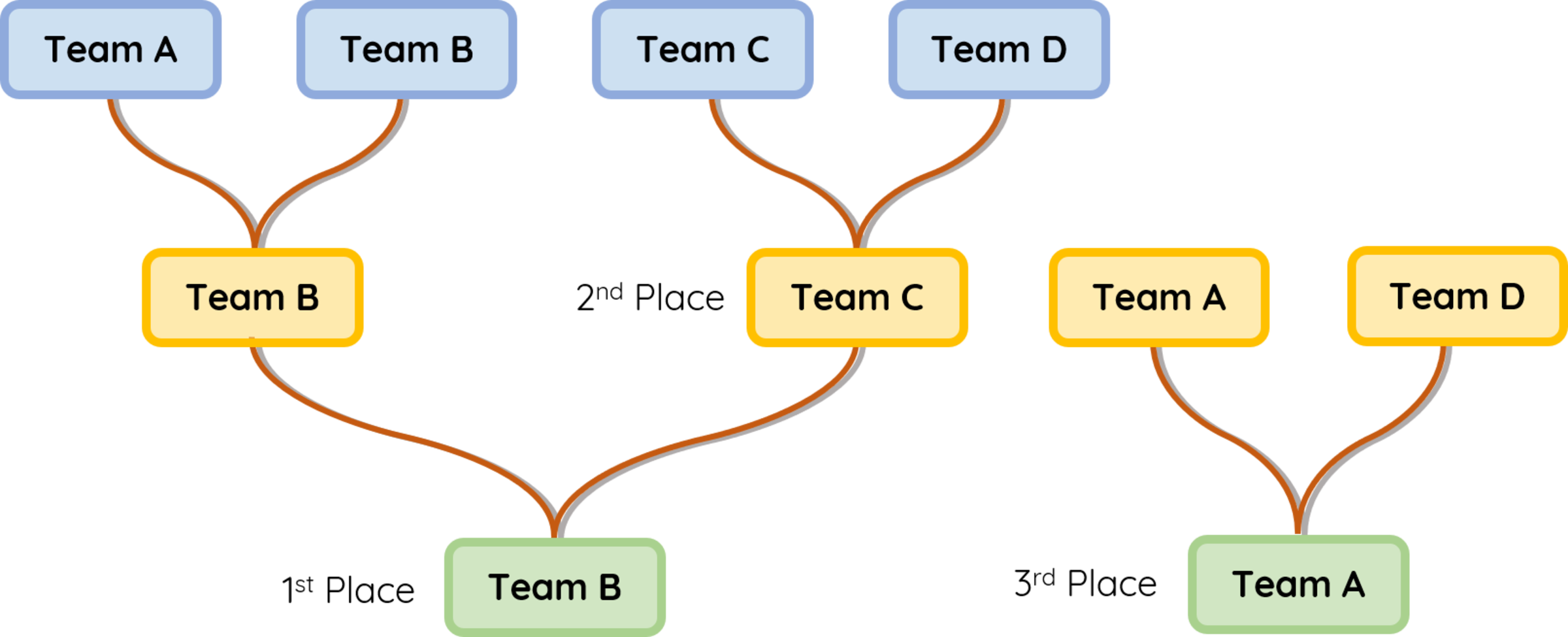Single Elimination Tournament
In a Single Elimination Tournament , teams are eliminated if they lose and the top 2 are determined with the finals while the 2nd runner up is determined with a game between the losers of the semi-finals.
However, this system is known to not properly rank teams. For instance, the 2nd best team should be winning 2nd but they can be eliminated in the first round if they played against the best team and hence not win anything.
Say there are teams competing. You are tasked to arrange games among the teams in order to accurately rank all teams based on their ability. You are allowed to change the teams taking part in future games based on results of the previous games. Assume that only 1 game is required to determine which team is better (E.g. if Team 1 and Team 2 play against each other and Team 2 wins, Team 2 is better at the game than Team 1), and that a game consists of teams and there will always be a winner, never a draw.
What is the minimum number of games that you have the arrange in order to guarantee that you can rank all teams?
The answer is 26.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
We can establish a lower bound for the number of games needed. Say there are n games needed. The number of possible outcomes for all n games are 2 n . Let the set of all outcomes of the games be G , ∣ G ∣ = 2 n . There are also 1 1 ! = 3 9 9 1 6 8 0 0 number of ways to rank the 1 1 teams. Let the set of possible rankings be R , ∣ R ∣ = 1 1 ! .
Now, there must exist an element g ∈ G such that from g we can deduce any ranking r ∈ R of the teams. In other words, for any r ∈ R , there must exist a g ∈ G such that g implies r .
Hence ∣ G ∣ ≥ ∣ R ∣ , 2 n ≥ 1 1 ! . This makes our lower bound to be n = 2 6 .
To prove that n = 2 6 is indeed possible, we can construct a solution with 2 6 games. We can reframe this question into a question involving sorting algorithms: Construct a sorting algorithm that can sort 1 1 elements with 2 6 comparisons. The Merge-insertion Sort achieves this and is therefore a valid construction. Hence it is possible to rank the 1 1 teams in 2 6 games.