Properties of circle part-2
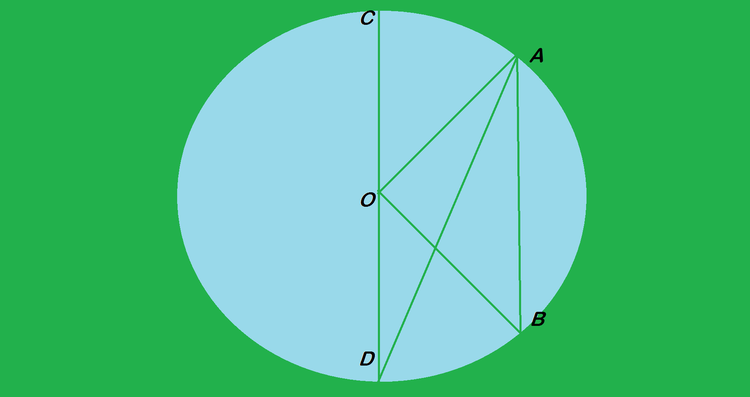 In the figure ,
O
is the centre of the circle and
CD
is parallel to
AB
. If
∠
D
A
O
=
2
0
∘
, then
∠
A
O
B
?
In the figure ,
O
is the centre of the circle and
CD
is parallel to
AB
. If
∠
D
A
O
=
2
0
∘
, then
∠
A
O
B
?
The answer is 100.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Nice one
As △ O A D is isosceles, we have ∠ O D A = 2 0 ∘ and, as C D ∥ A B , we have ∠ D A B = 2 0 ∘ .
Therefore, as △ O A B is isosceles, we have ∠ O B A = 4 0 ∘ and, hence, ∠ A O B = 1 0 0 ∘
Just focus on triangle DOA, since it is an isosceles triangle, angle A and D are equal to 20 deg, and angle O is 140. OA and OB are also equal, so it means that it also have equal angles. So make a perpendicular line from point O to line AB, from that you made a 90 deg angle, subtract 90 from 140 then multiply it by two, then youll get 100 degrees
Given that,
CD||AB
<DAO=20 degrees
In this circle,
radius,OA=OB=OC=OD
In triangle AOD
OA=OD
so,<ODA=<OAD
therefore,<ODA=20 degrees (given that,angle DAO=20 degrees)
again, as CD||AB
so, <CDA=<DAB (as,they are alternative angles)
=> <ODA=<DAB
so, <DAB=20 degrees
now, <OAD=20 degrees,<DAB=20 degrees
so,<OAB=<OAD+<DAB =(20+20) degrees =40 degrees
again,in triangle OAB
OA=OB (as they are radius)
so,<OBA=<OAB
therefore,<OBA=40 degrees
in triangle OAB
<OAB+<OBA+<AOB=180 degrees
=> <AOB+80 degrees=180 degrees
so,<AOB=100 degrees
Join AC
then ∠ C A D = 9 0 ∘ (because CD is diameter)
Then ∠ C A O = 7 0 ∘ .
△ CAO is an isosceles △ because OA and OC is radius.
∠ O C A = ∠ O A C
∠ O C A = 7 0 ∘ Then ∠ C O A = 4 0 ∘ (Angle sum property)
∠ C O A = ∠ O A B (Alternate interior angle)
∠ O A B = ∠ O B A ( OA = OB )
So, ∠ A B C = 1 0 0 ∘