Proportion of trailing zeros of factorials

Number Theory Level 3

$5!=120$ . Note that $\frac{1}{3}$ of the digits of this number are trailing zeros

$6!=720$ and again $\frac{1}{3}$ of the digits are trailing zeros

$7!=5040$ which is only $\frac{1}{4}$ trailing zeros (the zero in the hundreds place does not count as trailing.)

Consider the proportion of trailing zeros of $n!$

Which statement is correct?

$A$ : $6$ is the largest number whose factorial is $\frac{1}{3}$ trailing zeros and none have a higher proportion

$B$ : Other factorials beyond $6$ are $\frac{1}{3}$ trailing zeros, but none have a higher proportion

$C$ : There are a finite amount of numbers whose factorials are more than $\frac{1}{3}$ trailing zeros

$D$ : There are an infinite amount of numbers whose factorials are more than $\frac{1}{3}$ trailing zeros

B

D

C

A

3 solutions

Giorgos K.
May 9, 2018

Here is a $Mathematica$ code that computes the proportions

Table[Last@@Select[FactorInteger[k!],#[[1]]==5&]/IntegerLength[k!],{k,5,50}]

$\frac{1}{3},\frac{1}{3},\frac{1}{4},\frac{1}{5},\frac{1}{6},\frac{2}{7},\frac{1}{4},\frac{2}{9},\frac{1}{5},\frac{2}{11},\frac{3}{13},\frac{3}{14},\frac{1}{5},\frac{3}{16},\frac{1}{6},\frac{4}{19},\frac{1}{5},\frac{2}{11},\frac{4}{23},\frac{1}{6},\frac{3}{13},\frac{2}{9},\frac{6}{29},\frac{1}{5},\frac{6}{31},\frac{7}{33},\frac{7}{34},\frac{7}{36},\frac{7}{37},\frac{7}{39},\frac{8}{41},\frac{4}{21},\frac{2}{11},\frac{8}{45},\frac{8}{47},\frac{3}{16},\frac{9}{50},\frac{9}{52},\frac{9}{53},\frac{9}{55},\frac{10}{57},\frac{5}{29},\frac{1}{6},\frac{5}{31},\frac{10}{63},\frac{12}{65}$

here is a graph of the proportions of the first 50 factorials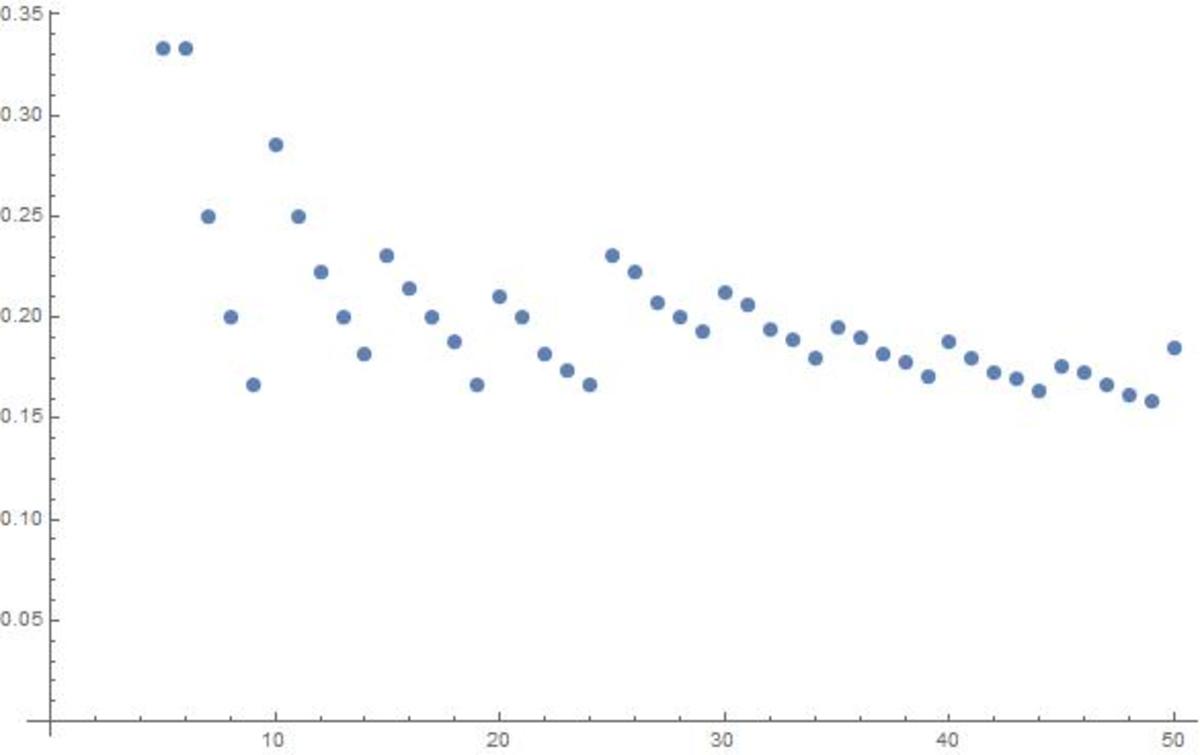

and the graph of 1000 factorials

Jeremy Galvagni
Apr 21, 2018

To add more zeros requires more factors of 5. To increase the proportion of zeros requires the number of digits to not increase, or at least increase more slowly.

10! ends in 2 zeros but is 7 digits long. 28.6%

15! ends in 3 zeros but is 12 digits long. 25%

20! ends in 4 zeros but is 19 digits long. 21%

25! ends in 6 zeros but is 26 digits long. 23%

Although the proportion can sometimes increase, it is a losing battle. Zeros increase on average once every 4 numbers (1/5 + 1/25 + ...) Total digits increase every time by at least 1.

Saad Khondoker
Feb 6, 2021

We don't need to compute a lot of numbers. To get an additional trailing $0$ in $n!$ we need last digit of $n$ to be $0$ or $5$ . This is true because, $10$ can be factored $5*2$ . So we need a $2$ and a $5$ to make a $10$ and multiplying $10$ gives us trailing zeros. A number ending with $5$ is divisible by $5$ and one of the even numbers will provide a $2$ .

Now, $10!$ will give the next trailing $0$ . If we check it, it has a proportion $2/7$ which is slightly lower than $6$ . The next trailing $0$ will be found in 15!. But for this trailing $0$ we had to multiply $5$ numbers greater than $10$ so $15!$ is at least $5$ digit greater than $10!$ . So the proportion is at most $3/12$ . The following numbers which will bring an additional $0$ can be eliminated with the same logic.

[Here, some might say what about the power of $5$ like $25$ and $125$ , they will give $2$ zeros and $3$ zeros respectively. But for a few additional $0$ s, more and more non zero numbers are added, so it will never catch up.]

Proportion of trailing zeros of factorials

3 solutions

0 pending reports