Unusual Proportions
If for three distinct positive numbers x , y and z ,
x − z y = z x + y = y x ,
then find the numerical value of y x .
AHSME 1992.
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Adding the numerators and denominators of the first two expressions yields a fraction equal to the original expression.
x − z y = z x + y = y x = x x + 2 y
Considering the last two expressions and letting m = y x gives m = 1 + 2 / m The previous equation results to m = 2 . Note that x and y are positive numbers.
Yay to Componendo and Dividendo !
From y/(x-z) =x/y, we have y^2= x^2-zx (1) From (x+y)/z= x/y, we have zx= xy+y^2 (2) Substituting the value zx in (1) x^2-xy-2y^2=0, x=2y or x= -y. Since x and y are both positive integers, x must be equal to 2y. Thus x/y= 2
Moderator note:
At which point did you use the fact that the integers were positive? Is that assumption necessary?
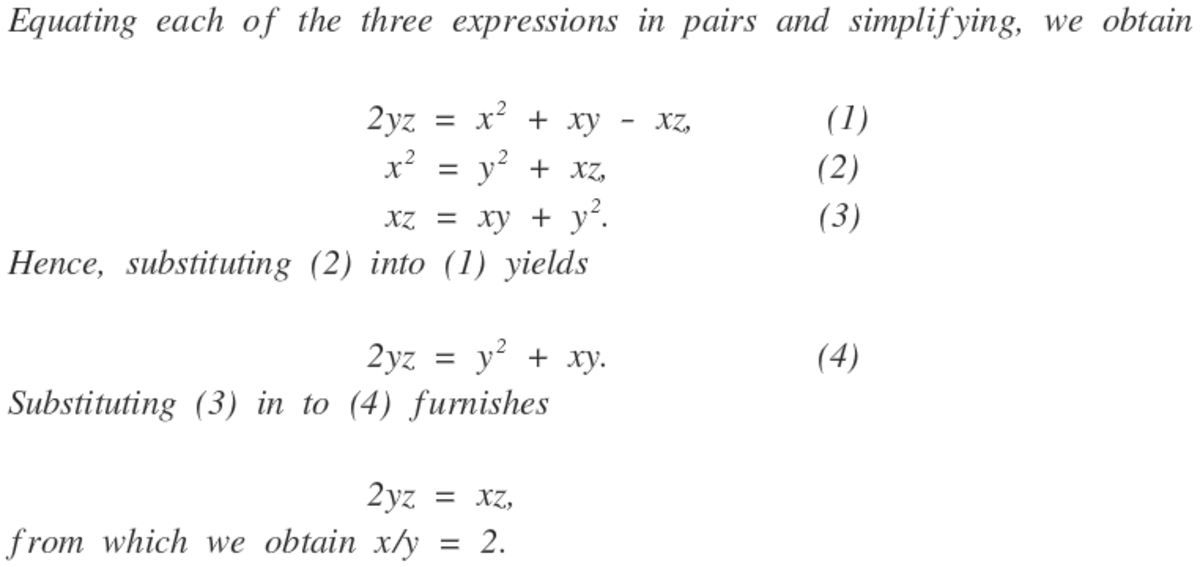
Suppose x − z y = z x + y = y x = c with c constant. So we have, y = c ( x − z ) … ( 1 ) x + y = z c … ( 2 ) x = y c … ( 3 ) subtituting ( 1 ) in to ( 2 ) x + c ( x − z ) = z c … ( 4 ) subtituting ( 3 ) i n t o ( 4 ) y c + c ( y c − z ) = z c c = y 2 z − y … ( 5 ) subtituting ( 5 ) in to ( 3 ) x = y y ( 2 z − y ) x + y = 2 z … ( 6 ) subtituting ( 6 ) in to ( 2 ) we have c = 2 . y x = 2