Protein Origami
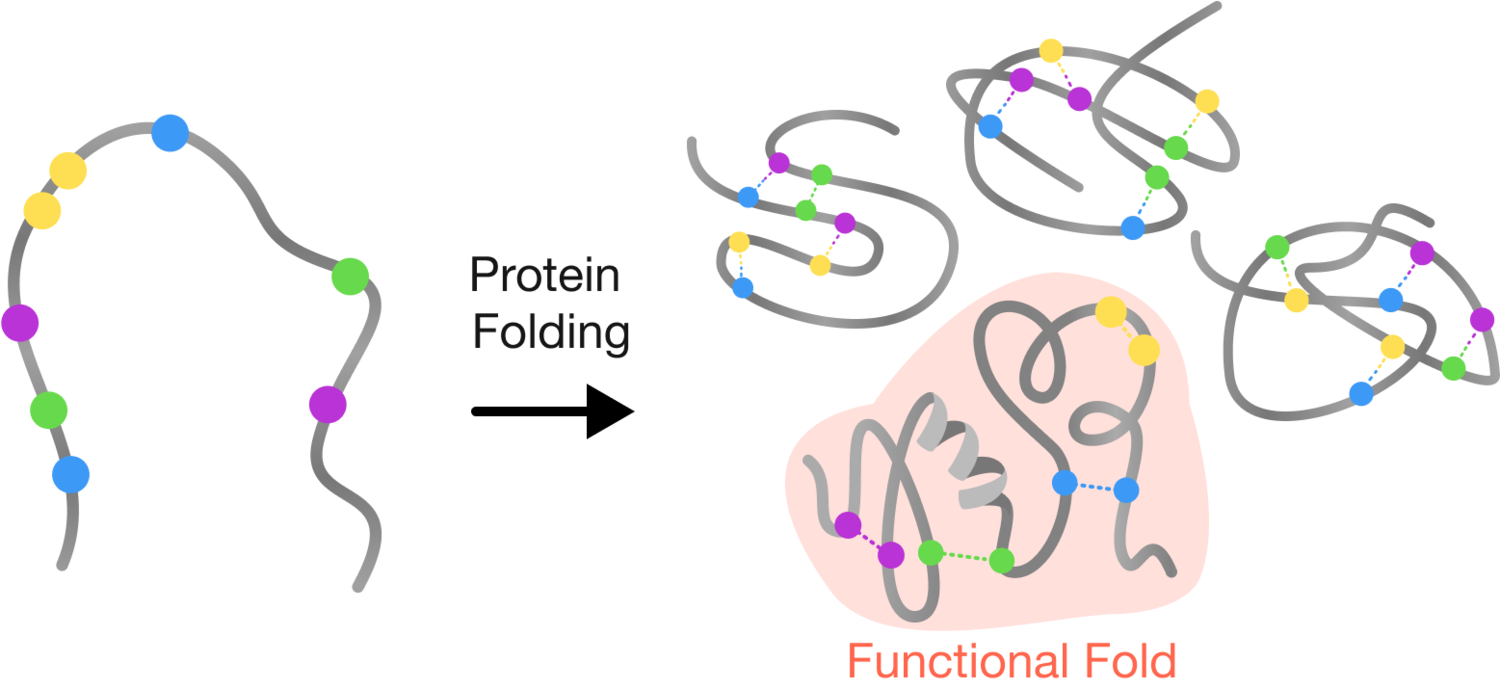
Out of the 1 2 4 amino acids that make up the ribonuclease enzyme, there are 8 cysteines . These amino acids can come together like velcro to form strong bonds that hold a protein into one folded configuration. A cysteine can form a bond with any other cysteine, and every cysteine is always paired; so the enzyme has a total of four bonds.
Only one arrangement of bonds will yield a correctly folded and functional ribonuclease enzyme capable of chopping up RNA molecules. In most cases, this folding process does not depend on the order that the bonds are formed.
If each protein randomly folds into one arrangement, what fraction of enzymes will be functional?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Great to see someone else approached this in same way I did - especially when it works!
Log in to reply
It's just a matter of thinking about it rather than searching the memory for an applicable theorem.
There are 8 ! ( where the ! symbol denotes the factorial ) ways to pair up the 8 cysteine amino acids. This number of ways includes different orderings of the same two cysteines, so we must divide by 2 because the ordering of the C amino acids in each pair is unimportant. We must divide by 4 ! because the ordering of the pairs as a whole is unimportant to the structure of the protein.
Thus, the number of arrangements is given by 2 4 × 4 ! 8 ! = 1 0 5 .
If each protein folds randomly, we'd expect only 1 0 5 1 < 1 % of the proteins to find this functional fold. In fact, basically 1 0 0 % of ribonuclease enzymes fold into the correct arrangement. How proteins stumble onto their so-called "native" fold is still a field of active study.
You wrote, "because the ordering of the pairs as a whole is unimportant to the structure of the protein." I doubt that assumption is justified.
I think this problem is poorly posed.
The expected answer fails to consider whether the pairs were correctly matched in the wrong sequence. For example, in paper folding instructions, putting tab A in slot B first, followed by putting tab C in slot D after, will not necessarily always give the same result as putting tab C in slot D, first, and putting tab A into slot B after. It depends on the specific details of what shape is being folded. The sequence of steps can affect whether certain layers end up inside or outside of other layers, even if we don't change which tabs go into which slots. I do not see why that principle would be any different for proteins.
Log in to reply
That's certainly a reasonable doubt. I've added that assumption to the problem statement. To clarify: there are some cases in which proteins can fold into topological knots, which are often stabilized by disulfide bonds. In these cases the order of bond formation certainly matters. Generally speaking though, these cases are few and far between.
Of course, since this is a basic level solvable we've had to make assumptions like this to simplify the problem. In reality, the formation of a correct disulfide arrangement does not guarantee the protein folds properly. In fact, this exact combinatorial problem was one performed by Christian Anfinsen when he first studied protein folding. He found that spontaneous folding of the rest of the protein conspires to form the correct arrangement of disulfides, rather than the arrangement of disulfides forming the correct protein fold.
Check out this Brilliant problem set on protein folding and the Anfinsen experiment if you're interested: Protein Origami .
Why would the order of the bond formation necessarily make a difference?
Proteins aren't like paper when it comes to folding. Proteins are long chains of amino acids - basically they are better modeled as strings (at least the primary structure before folding) than as a two-dimensional surface like a piece of paper.
Protein folding happens in multiple stages, and this question only concerns itself with the first stage.
Hi Blake, did you divide by 2^4 because the order in each of the 4 pairs wasn’t important? I solved this a different way. Is this correct?
First, I did 8 ncr 4 because there are the 8 cysteines and we want them to be paired, so this would make 2 groups of 4 (the four chosen and the four remaining). Then, I multiplied that by 2( 4 ncr 2) because we needed to make a pair in each of the groups of 4. This resulted in 105, and since only one of the combinations worked, I chose 1/105.
Log in to reply
Hi Matthew-
Yep, I divided by 2 4 because there are two ways of ordering each pair, and their order doesn't matter. Without this factor, we'd be over-counting.
If i'm understanding your approach correctly, you took ( 4 8 ) × 2 × ( 2 4 ) . This results in 8 4 0 , not 1 0 5 . Starting with the binomial makes sense for this problem, but you can't do another binomial for making the pairs. You could however use the multinomial , which is used when you're looking at the number of ways to put a some number of objects into boxes. You can check out Brilliant's wiki on Multinomials here .
Log in to reply
Oh okay. I meant to put a carrot for (4 ncr 2) ^2 = 36. I divided (8 ncr 4) by an extra 24 by accident, then multiplied it by the 36 and got 105. I understand your solution, which is what counts! Thank you for your feedback. :)
What I thought was..... Out of ( 8C2 x 6C2 x 4C2 x 2C2 ) ways of selecting pairs of cysteines,only one is correct. But it is entirely different. I don't know why.
Log in to reply
It is not so that only 1 is correct, because when you do 8C2 the first time you are picking a pair and saying that you must always pick that specific pair first. In fact it you can pick any of the 4 pairs so instead you should do 8C2/4 for the first one, 6C2/3 for the second, and 4C2/2 for the third. Multiplying these gives the correct answer.
I follow Marta’s answer, OK. But 8C2 = 28 and 8P2 = 56, how then can there by so few ways of picking 2 from 8?
Blake’s answer, oh... i finally get that too.
But still stumped WHY the concept of ‘choose’ or ‘permutations’ of 2 from 8 are so wrong. What’s the correct thinking, i can’t find my old Discrete Math book
I couldn't understand the question at all, not having studied protein folding before. The question talks about amino acids and enzymes and then suddenly asks about a protein, what is the protein in relation to this? Are the other 116 amino acids relevant in any way? The answer is the number of ways that 8 DISTINCT objects can pair up, but I didn't see anything in the question to indicate that the the cysteins had an identity. I get the impression from reading the answers that the cysteins are ALSO bonded to the other 116 acids and they form a second bond with each other but there was no way to know this from the question? This would mean there were hundreds of bonds in the thing but the question clearly said there were only 4 bonds. A bit more background would be appreciated :( I am quite confused right now.
Log in to reply
Yes, also. Even if there had been more clarification, this problem would deserve to be placed higher than in "Basic."
The number of perfect matchings of a complete graph K n for n even is given by ( n − 1 ) ! ! where ! ! stands for the double factorial .
So here, for eight nodes, we have 7 ! ! = 7 ∗ 5 ∗ 3 ∗ 1 = 1 0 5 possible matchings and only one of them yields a correct folding. Hence the fraction is 1 0 5 1
High quality way of transmitting maths to language. Wonderful, thx. Peter.
Consider all the cysteines.
When there are 8 cysteines, we can choose whatever you want as a beginning and then there is a only one can fit it. For 7 1 chance.
And there are 6 cysteines left, we still can choose one randomly, after that a only one fit it, the possibility is 5 1 .
The same situation when 4-3 cysteines and 2-1 cysteines.
So we can list one expression as follow
1* 7 1 * 1 * 5 1 * 1 * 3 1 * 1 * 1 1 = 1 0 5 1
Events:
- First. The probability of selecting the first cysteine is 1 because you can pick up any of them.
- Second. The probability of selecting its only partner is 7 1 because you need to pick the exact one you need in seven options you have.
- Third. The probability of selecting the third cysteine is 1 because you can pick up any of the six remaining.
- Fourth. The probability of selecting the only partner of the third random cysteine is 5 1 .because you need to pick the exact one you need in five options remaining.
Now we can see how the events to follow have to happen if we want only one configuration, and because each one of the events is independent we can multiply their probability to obtain the probability of the composite event which will mean a certain arrangement.
1 ∗ 7 1 ∗ 1 ∗ 5 1 ∗ 1 ∗ 3 1 ∗ 1 ∗ 1 1 = 1 0 5 1
Most excellent! I like how you explained this. I tried to wrap my head around it, and your explanation gave a comfortable method of math to use. Big yeah! Thank You . Cheers, Melissa
Log in to reply
Thanks a lot, I really apriciate your feedback and cheers, this is my very first solution posted, and makes me very happy to know that you like my explanation. Big hug -> Pablo
In general, we can calculate fractions of these kind as follows: N u m b e r O f P o s s i b l e C o m b i n a t i o n s N u m b e r O f W a n t e d C o m b i n a t i o n s
Now, lets imagine the bonds as a "chain". Two cysteine bond together if they are right next in the chain.
For the number of possible combinations we just have 8 factorial since there are 8 cysteines whose arrangement doesn't matter (yet).
To find the number of wanted combinations is a bit trickier:
For first one in the "chain" we can pick any of the cysteines.
For the second one we only have one choice: The other cysteine of the same kind.
For the third one we can pick any of the remaining ones and so on.
That leaves us with the following fraction: 8 ! 8 ∗ 1 ∗ 6 ∗ 1 ∗ 4 ∗ 1 ∗ 2 ∗ 1 = 1 0 5 1
Pick any particular cysteine. It has to be bonded with just one other cysteine, and it has to be the correct one. There is 7 1 chance that it is so since there are 7 possibilities.
This takes care of two of the cysteines. Pick any of the remaining six. This cysteine too has to be bounded with the right one, and the chance of that is 5 1 .
Selecting one of the remaining 4 to consider, it has 3 1 chance of being connected correctly.
Finally, the last two have to be correct, if all else is. So the chance of them being right is 1 .
The probability of all the bonds being correct simultaneously is the product, that is 7 1 ⋅ 5 1 ⋅ 3 1 ⋅ 1 = 1 0 5 1