Prove this?
If k = 2 p − 1 , where p > 1 , and N = k 2 − 1 , is 2 p + 1 a factor of N ?
In your solution, provide a complete proof
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Can you elaborate on the last step after stating that p > 1? Like how did you come to the fact that 2 p ( 2 p − 2 ) = 2 p + 1 ( 2 p − 1 − 1 )
Log in to reply
Take a 2 common from the bracket
I have added a line. Hope that it helps.
Log in to reply
Sir, can you please post a solution for this: https://brilliant.org/problems/confusing-question-no-way-out/ ; posted by @Syed Hamza Khalid
I am unable to understand it. Tbh, your solutions are the best; I always understand it thx to your amazing talent and use of colours
Oh yes sure thanks a lot
Brilliant - but there's a small typo; you should have 2 p − 1 − 1 at the end.
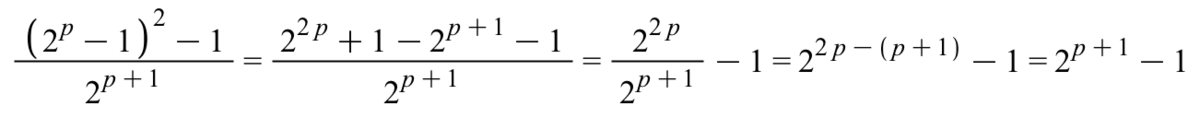
N = k 2 − 1 = ( k + 1 ) ( k − 1 ) = 2 p ( 2 p − 2 ) = 2 p ⋅ 2 ( 2 p − 1 − 1 ) = 2 p + 1 ( 2 p − 1 − 1 ) As k = 2 p − 1 Note that p > 1
Yes , 2 p + 1 is a factor of N .