Pruning the Harriss Tree
The Harriss spiral as shown in this graphic is a fractal, where all the white boxes are perfect squares, and all colored boxes are all similar, i.e., even the grey and beige boxes are similar. The entire rectangular enclosure is similar to any of the colored nonwhite boxes.
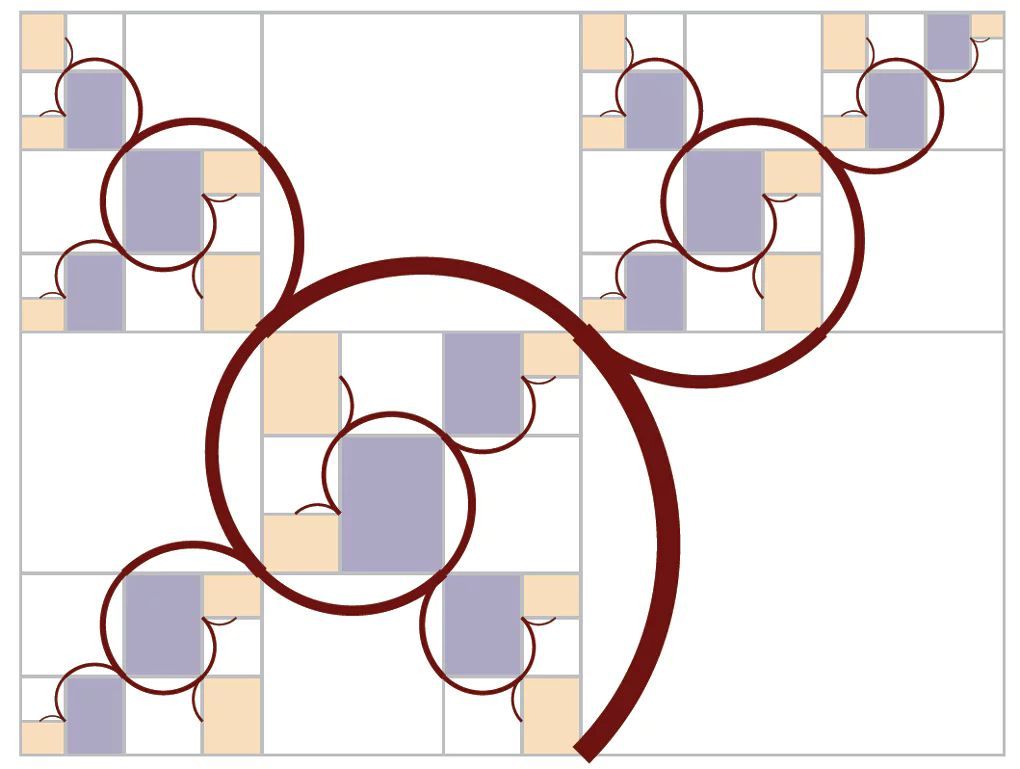
Each colored box only indicates further subdivision by white squares in the same fractal pattern. When reiteration is done infinitely many times, there are only white squares that make up the entire rectangular enclosure.
In each white square there are two brown branches, both quarter circle arcs, but of two different sizes. A botanist decides to study the Harriss [spiral] tree by first cutting all the brown quarter circle segments (BQCS) at the corners of the squares, so that each white square yields 2 BQCSs. He has a row of many boxes. Inside the first box, he puts the one largest BQCS. Inside the second box, he puts in the next largest BQCS. In each box, he puts in all BQCSs of the same size, so that all of the sizes are sorted in a row in progressively smaller sizes, starting with the largest size. The botanist wants to study the distribution of BQCS sizes.
How many BQCSs are there in all of the first 12 sizes, that is, in the first 12 boxes, total?
Note: This Harriss spiral involves the plastic number which is often called the forgotten cousin of the golden ratio .
The answer is 187.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The distribution of the BQCSs follows the Narayana's Cow Sequence (not to be confused with Narayana Numbers)
1 , 1 , 1 , 2 , 3 , 4 , 6 , 9 , 1 3 , 1 9 , 2 8 , 4 1 , 6 0 , 8 8 , 1 2 9 , . . .
except for the first term. The sum from the 2 nd term to the 1 3 th term is 1 8 7
The distribution of the sizes of the white squares also follows the same sequence, except that it does include the first term, i.e., there's one one of each of the first 3 three largest sizes.
This sequence in similar to the Fibonacci Sequence, except that a n = a n − 1 + a n − 3
Incidentally, the total length of all the BQCSs is infinite. Meanwhile, the sum of all the white squares add up to the area of the entire rectangular enclosure, exactly.
Edit:
Let q be a constant that is a ratio of the side lengths of two successive sizes of white squares. It is immediately seen that because of the fractal self-similarity of the Harris "Rectangle" (which shall refer to the entire rectangular enclosure) that the sizes of the white squares are 1 , q , q 2 , q 3 , . . . as seen in the graphic. Note that the rectangles adjacent to both the top and the left side of the square of side length 1 are of the same size, so that we can infer size of that square marked q 3 on the top border of the square of side length 1 . Thus, every white square in the Harris Rectangle has a side of q n , where n is a positive integer.
The actual value of q is not really relevant to this problem (but we will get to that later anyway). From the graphic we can see that the two BQCSs in the largest white square have a tip-to-tip width of 1 and q 2 . In other words, in any white square of side q n , the larger BQCS has that size, while the lesser BQCS has the size q n + 2 . Moreover, every square "points" to two more squares, of sizes q n + 1 and q n + 3 , so, we can sketch out a tree of BQCS generation as follows
where each line from the top lists the numbers and sizes of new BQCSs being generated. One can see the parallel with Pascal's Triangle. The next step is adding up the numbers of each size BQCS, and, again, there is a clear pattern where to find BQCSs of the same size. We can rearrange the triangle above to rows to be added, with the total shown at the bottom
so that we can see that the coefficients follow the Narayana's Cow Sequence, as described above. Consider two sizes q n and q n + 2 . Each instance of size q n will "point" to a square containing one BQCS of size q n + 3 , and similarly, each instance of size q n + 2 will "point" to a square containing one BQCS of size q n + 3 , and no two BQCSs point to the same square. Hence, the coefficients of the totals line a n and a n + 2 add up to a n + 3 , which is the recurrence equation of the Narayana's Cow Sequence. The sum of the first 1 2 coefficients in this sequence is 1 8 7 .
In fact, using the way the rows add up to the Narayana's Cow Sequence as shown here, we can derive a mathematical expression for generating the sequence (which starts with 1 , 1 , 1 , . . . ) as follows
k = 0 ∑ ⌊ 3 n ⌋ ( n − 1 − 2 k k ) = ( 1 , 1 , 1 , 2 , 3 , 4 , 6 , 9 , 1 3 , 1 9 , 2 8 , 4 1 , 6 0 , 8 8 , 1 2 9 , . . . )
Now let's find out what q equals to. First, from the marked graphic shown above, we note that
1 = q 2 + q 3
or
( q 1 ) 3 = q 1 + 1
Let p = q 1 . Then we have
p 3 = p + 1
with the solution
p = 3 1 8 1 ( 3 9 + 6 9 + 3 9 − 6 9 ) = 1 . 3 2 4 7 1 7 9 5 7 . .
which is the Plastic Constant . "Plastic Number" and "Plastic Constant" are used interchangeably. This number p is the ratio of the sides of the entire rectangular enclosure.