Ptolemy's Riddle II
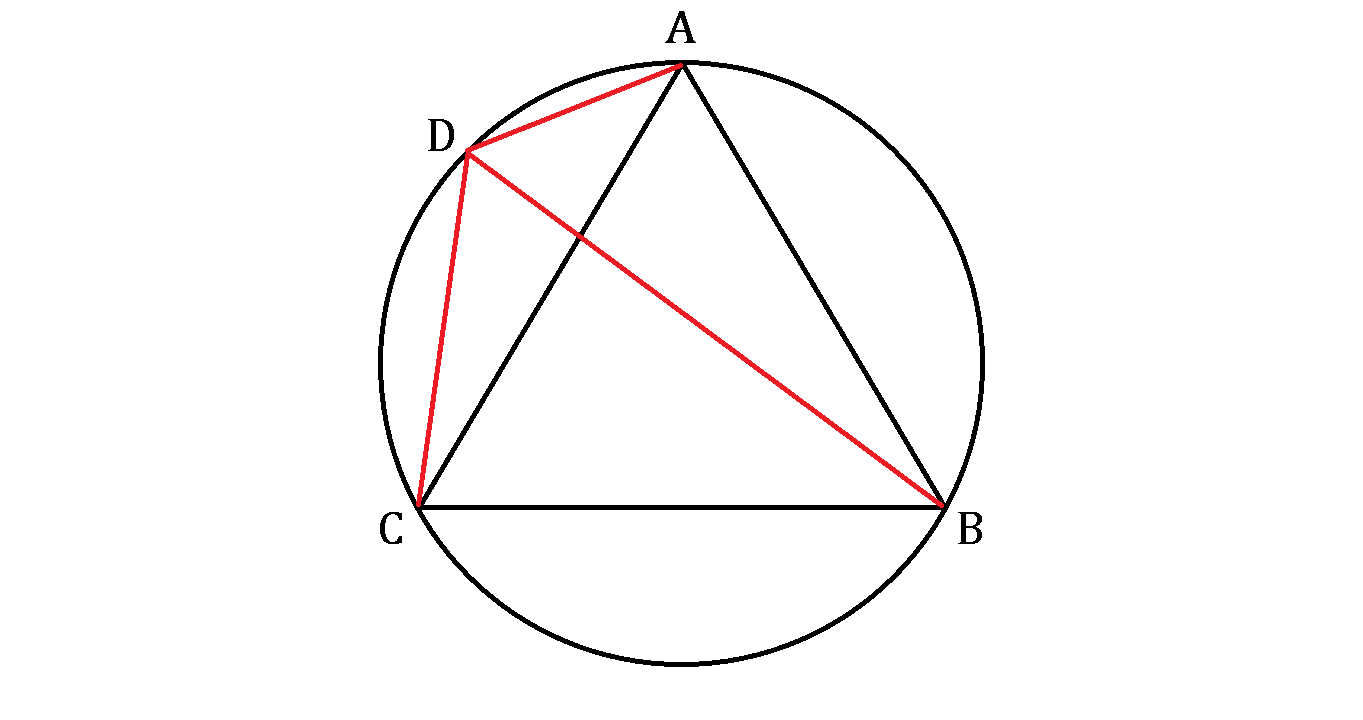
Once upon a time, Ptolemy let his pupil draw an equilateral triangle A B C inscribed in a circle before the great mathematician depicted point D and joined the red lines with other vertices, as shown below.
Ptolemy
: Dost thou see that all the red lines have the lengths in whole integers?
Pupil
: Indeed, master! Such an extraordinary point!
Ptolemy
: Now if the equilateral triangle has a side length of 13, what is the sum of the three red lengths combined?
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
is there any other way to do this without using congruences ???
Log in to reply
Given n<26, we can check for all possible values by brute force, but with modular congruence, it helps save time.
think of the limit as D tends to A then ADC =13 and ADB =13 so the sum must be 26 since it is constant and independent of the position of D
Very helpful Sir thanks
I used a similar method first, but then i took an ideal approach and took BD as the diameter. Then the answer to the question came out to be approximately 30.02, but it said the answer was integer, so i approximated it to 30.
I used ptolemy's second theorem which narrowed the possible values of the longer diagonal to be 14,15,16 and 17.
 Imgur
Imgur
Let the red lengths be a, b and c as shown. 13 < b < diameter = 3 2 × 1 3 = 1 5 . 0 1 1 and it has to be an integer. So it must be 14 or 15. Just two possibilities! Cheap enough for trial and error :-)
Moreover, ∠ A D B = ∠ C D B = 6 0 ° Hence, cos A D B = 2 1 = 2 a b a 2 + b 2 − 1 3 3 Try b = 14 and 15 only b=15 gives integer values of a = 7 or 8. So if a = 7, c must be 8 or vice versa. But irrespective of that the sum of the three red lengths is 7 + 8 + 15 = 30.
In face, Ptolemy could have been more impressive by saying, "And there is one more point that does it!" :-) (of course, that follows from symmetry too.)
Let DA=a and DC=b
Angle ADC=120*
From cosine rule,
a 2 + b 2 + a b = 1 3 2 = 1 6 9
( a + b ) 2 − a b = 2 2 5 − 5 6
( a + b ) 2 − a b = ( 7 + 8 ) 2 − ( 7 ∗ 8 )
On comparing,
a=7,b=8
From Ptolmey's theorem,
13a + 13b = 13.BD
Therefore, a+b = BD
a+b+BD = 2(a+b)
=2(7+8)
=30
thanx a lot bro
1- realize that DA=DC from equal angles of 60° facing same arcs respectively
2- apply Ptolemy's Theorem so that DB=DC+DA= 2DA
3- apply cosine law in ACD triangle to get that DA = 13/SQRT(3)
4- Sum = 4 DA = 52/sqrt(3) = 30
Since A B C D is a cyclic quadrilateral, ∠ C D A + ∠ C B A = 1 8 0 ∘ . And since A B C is an equilateral triangle, ∠ C B A = 6 0 ∘ . Then ∠ C D A = 1 2 0 ∘ ).
By using cosine rule, A C 2 = 1 3 2 = 1 6 9 = C D 2 + D A 2 − 2 ( C D ) ( D A ) ( cos 1 2 0 ∘ ) = C D 2 + D A 2 + ( C D ) ( D A )
Let C D = x and D A = y for some integers x , y . We can then set up a quadratic equation:
x 2 + x y + ( y 2 − 1 6 9 ) = 0
The quadratic residue must then be perfect square: y 2 − 4 ( y 2 − 1 6 9 ) = n 2 for some integer n .
Thus, 2 6 2 − 3 y 2 = n 2 .
2 6 2 − n 2 = 3 y 2
( 2 6 − n ) ( 2 6 + n ) = 3 y 2
2 6 − n > 0 . n < 2 6
If 2 6 − n ≡ 1 ( m o d 3 ) , then 2 6 + n ≡ 0 ( m o d 3 ) .
If 2 6 − n ≡ 0 ( m o d 3 ) , then 2 6 + n ≡ 1 ( m o d 3 ) .
Thus, n is not a multiple of 3 .
If n = 2 3 , then y = 7 . Then x = 8 .
Then by Ptolemy's Theorem , D B × 1 3 = 1 3 × 7 + 1 3 × 8 .
Thus, D B = C D + D A = 7 + 8 = 1 5 .
As a result, D C + D B + D A = 3 0 .