Ptolemy's Riddle III
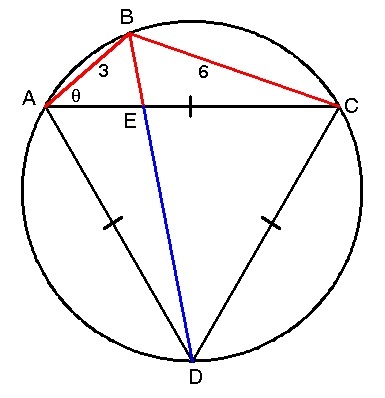
A cyclic quadrilateral A B C D is constructed within a circle such that A B = 3 , B C = 6 , and △ A C D is equilateral, as shown to the right.
If E is the intersection point of both diagonals of A B C D , what is the length of E D , the blue line segment in the diagram?
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
The "combined theorems solution" was nice, I liked it a lot !
Complicate
Since quadrilateral ABCD is cyclic, ∠ A B C = ( 1 8 0 − ∠ A D C ) ∘ = ( 1 8 0 − 6 0 ) ∘ = 1 2 0 ∘ . Also, ∠ A B D = ∠ A C D ⟹ ∠ A B D = ∠ C B D = 6 0 ∘ . Using the Law of Cosines , we see that A C 2 = A B 2 + B C 2 − ( 2 ⋅ A B ⋅ B C ⋅ cos ( ∠ A B C ) ) A C 2 = 3 2 + 6 2 − ( 2 ⋅ 3 ⋅ 6 ⋅ cos ( 1 2 0 ∘ ) ) A C 2 = 9 + 3 6 − ( 3 6 ⋅ − 2 1 ) A C 2 = 4 5 + 1 8 = 6 3 A C = 6 3 = 3 ⋅ 7 To find the length of E D , we can use the Power of points Theorem , which, in our case, states that B E ⋅ E D = A E ⋅ E C . First, let's find A E ⋅ E C . Seeing that B D bisects ∠ A B C , by the Angle Bisector Theorem, we know that A E = 9 3 ⋅ A C = 3 1 ⋅ 3 ⋅ 7 = 7 and E C = 9 6 ⋅ A C = 3 2 ⋅ 3 ⋅ 7 = 2 ⋅ 7 Therefore, A E ⋅ E C = 7 ⋅ 2 ⋅ 7 = 7 ⋅ 2 = 1 4
Now, to find the length of BE, we can use the Law of Cosines to get A B 2 = B C 2 + A C 2 − ( 2 ⋅ A C ⋅ B C ⋅ cos ( ∠ A C B ) ) A B 2 − B C 2 − A C 2 = − ( 2 ⋅ A C ⋅ B C ⋅ cos ( ∠ A C B ) ) − 2 ⋅ 3 ⋅ 7 ⋅ 6 3 2 − 6 2 − 6 3 = cos ( ∠ A C B ) cos ( ∠ A C B ) = − 3 6 ⋅ 7 − 9 0 = 2 ⋅ 7 5 Using this information, we can use the Law of Cosines again to find B E B E 2 = B C 2 + E C 2 − ( 2 ⋅ B C ⋅ E C ⋅ cos ( ∠ A C B ) ) B E 2 = 6 2 + 4 ⋅ 7 − ( 2 ⋅ 6 ⋅ 2 ⋅ 7 ⋅ 2 ⋅ 7 5 ) B E 2 = 3 6 + 2 8 − ( 6 0 ) B E = 4 = 2 Plugging these into the original equation from the Powers of Points, we get 2 ⋅ E D = 1 4 E D = 2 1 4 = 7
B y P t o l e m y ′ s T h e o r e m B D ∗ A C = 3 ∗ C D + 6 ∗ A D , ⟹ B D = 9 . ∵ A C = C D = A D . U s i n g C o s R u l e i n Δ A B C , w i t h ∠ C B A = 1 8 0 − ∠ A D C o f c y c l i c A B C D = 1 2 0 , ∴ A C = 3 7 . ∠ s b y D C , ∠ C B D = ∠ C A D = 6 0 . ⟹ E B A = 1 2 0 − 6 0 = 6 0 , a n d B E a n a n g l e b i s e c t o r . ∴ B E = B A ∗ B C ( 1 − ( A B + B C ) 2 A C 2 ) = 3 ∗ 6 ( 1 − ( 3 + 6 ) 2 6 3 ) = 2 . E D = B D − B E = 9 − 2 = 7 .
Plz correct that / CBD =/ CAD in fourth line. Thanks for this solution
After you have shown BD = 9 and AC = AD = 3√7, you can also proceed by:
∆ADE is similar to ∆BDA (equiangular), since ∠ADB is common and ∠EAD = ∠ABD = 60°
Hence ED / 3√7 = 3√7 / 9, giving ED = 7
△ A E D and △ B E C are similar triangles as ∠ A D B = ∠ A C B and ∠ A E D = ∠ B E C .
So, E C E D = B C A D ⟹ E C = E D ⋅ A D B C
Again, △ A B E and △ D C E are also similar triangles.
So, E A E D = A B C D ⟹ E A = E D ⋅ C D A B
⟹ A C = E A + E C = E D [ A D B C + C D A B ]
Now, A C = A D = C D as △ A C D is equilateral.
⟹ A C = A C E D ( B C + A B ) ⟹ E D = B C + A B A C 2
But A B = 3 , B C = 6 , ∠ A B C = 1 8 0 ∘ − ∠ A D C = 1 2 0 ∘
⟹ A C 2 = 3 2 + 6 2 − 2 × 3 × 6 cos 1 2 0 ∘ = 9 + 3 6 + 1 8 = 6 3
So, E D = 6 + 3 6 3 = 7
Good method! Better than having to use Ptolemy's Theorem. You only used similarity and cosine law!
By Ptolemy's Theorem, B D × A C = 3 × C D + 6 × A D ⟹ B D = 9 .
∠ A B D = ∠ A C D = ∠ D A C = ∠ D B C = 6 0 ∘ .
By cosine rule, A D 2 = 3 2 + 9 2 − 2 × 3 × 9 × cos ( 6 0 ∘ ) ⟹ A D = 3 7 .
a r ( Δ A B C ) = 2 1 × 3 × 6 × sin ( 1 2 0 ) = 9 × 2 3 and a r ( Δ D B C ) = 6 3 × 4 3 .
a r ( Δ A B C ) a r ( Δ D A C ) = E B D E = 2 7 and D E + E B = 9 .
So, E D = 7 .
Yes, much similar to mine. Why don't you come online at Slack ?
By theorem ,
∠ A B C + ∠ A D C = 1 8 0
∠ A B C + 6 0 = 1 8 0
∠ A B C = 1 2 0
Apply cosine law at △ A B C :
A C 2 = 3 2 + 6 2 − 2 ( 3 ) ( 6 ) ( cos 1 2 0 )
A C 2 = 9 + 3 6 − 3 6 ( − 0 . 5 )
A C 2 = 6 3
A C = 6 3
A C = 3 7
3 ( 3 7 ) + 6 ( 3 7 ) = 3 7 B D
B D = 9
By intersecting chords theorem
( B E ) ( D E ) = ( A E ) ( C E )
However, C E = 3 7 − A E and D E = 9 − B E .
Substitute
( 9 − B E ) ( B E ) = ( 3 7 − A E ) ( A E )
9 B E − B E 2 = 3 7 A E − A E 2 ( 1 )
Apply cosine law at △ A B C :
6 2 = 3 2 + ( 3 7 ) 2 − 2 ( 3 ) ( 3 7 ) ( c o s θ )
cos θ = 7 2
Apply cosine law at △ A B E :
B E 2 = 3 2 + A E 2 − 2 ( 3 ) ( A E ) ( 7 2 )
B E 2 = 9 + A E 2 − 7 1 2 7 A E ( 2 )
Adding ( 1 ) and ( 2 ) , we obtain
B E = 7 7 A E + 1 ( 3 )
Substituting ( 3 ) in ( 2 ) , we obtain
7 6 A E 2 − 2 7 A E + 8 = 0 ( 4 )
Using the quadratic formula in ( 4 ) , we obtain
A E = 7
Substituting 7 for A E in ( 3 ) , we get
B E = 2
Finally,
E D = 9 − 2 = 7
Built a spreadsheet with two parameters -- the radius of the circle and the angle for B. A, C, and D are well defined from the radius. Modified the radius and the angle numbers until the distance from A to B was 3 and the distance from B to C was 6. Took just a couple of minutes. Then the ratio of the difference between the y component of (A - D) / (B - D) times the length of (B - D) is the answer. 7.
You have found that (A-D)/(B-D) is equal to 7 for specific parameters, how do you know that this expression can't have an alternative value?
By Ptolemy's theorem B E + E D = 9 and by the intersecting chords theorem B E ⋅ E D = A E ⋅ E C . By the cosine theorem A C = 6 3 and by the bisector theorem A E = 3 1 6 3 , E C = 3 2 6 3 . It follows that B E , E D fulfill B E + E D = 9 , B E ⋅ E D = 9 2 6 3 = 1 4 , so B E = 2 and E D = 7 .
Let A E = t and A B = B C = A C = s . Observe that △ A E D similiar with △ B E C . Then B E A E = B C A D ⟺ B E = A D A E × B C = 3 t s Observe that △ A B E similiar with D C E . Then B E A B = C E C D ⟺ t s / 3 s = s − t 6 We have s = 3 t , C E = 2 t , and B E = t 2 . Because A B E similiar with D C E , we have A E A B = D E A C ⟺ D E = B E C E × A E = t 2 2 t × t = 2 We will prove that B D = A D + D C . From Ptolemy's Theorem, A B × C D + A D × B C = A C × B D ⟺ A D + C D = B D Then B D = 3 + 6 = 9 . Therefore, B E = 9 − 2 = 7
By Van Schooten's Theorem, BD = 3 + 6 = 9
By Angle Bisector Theorem, AE : EC = 1 : 2
By Inscribed Angles Theorem, Angle ABC = 120 degrees
By Law of Cosines, AC = 3 sqrt 7
By Stewart's Theorem, BE = 2
Therefore, DE = 9 - 2 = 7.
Thank you po!
According to Inscribed Angles Theorem , ∠ D A C = ∠ D B C = 6 0 ∘ and ∠ A B D = ∠ A C D = 6 0 ∘ because the each angle of the equilateral triangle is 6 0 ∘ .
Therefore, the diagonal B D bisects ∠ A B C . Then suppose A B = a , B C = b , B D = d , A E = m , E C = n , and A C = c = m + n so according to Angle Bisector Theorem , a : b = m : n .
In other words, a ⋅ n = b ⋅ m .
Multiplying both sides by b − a , we will get: a ⋅ n ( b − a ) = b ⋅ m ( b − a ) .
Hence, a 2 n + b 2 m = a b ( m + n ) .
According to Ptolemy's Theorem , a c + b c = c d . Thus, d = a + b , or B D = A B + B C .
Now considering △ A B C , according to Stewart's Theorem , we can apply the variables, where B E = x as followed:
a 2 n + b 2 m = ( m + n ) ( x 2 + m n )
According to Two Secants Theorem , m n = x ( d − x ) = x ( a + b − x ) .
Hence, a 2 n + b 2 m = ( m + n ) x ( x + ( a + b − x ) ) = x ( m + n ) ( a + b ) .
Plugging in the first finding in the earlier equation: a 2 n + b 2 m = a b ( m + n ) = x ( m + n ) ( a + b )
Thus, x = a + b a b , or more specifically, x 1 = a b a + b = a 1 + b 1 .
Now substituting a = 3 & b = 6 , we will get:
x 1 = 3 1 + 6 1 = 2 1 . Thus, x = B E = 2 .
Finally, E D = 3 + 6 − 2 = 7 .