Ptolemy's Riddle IV
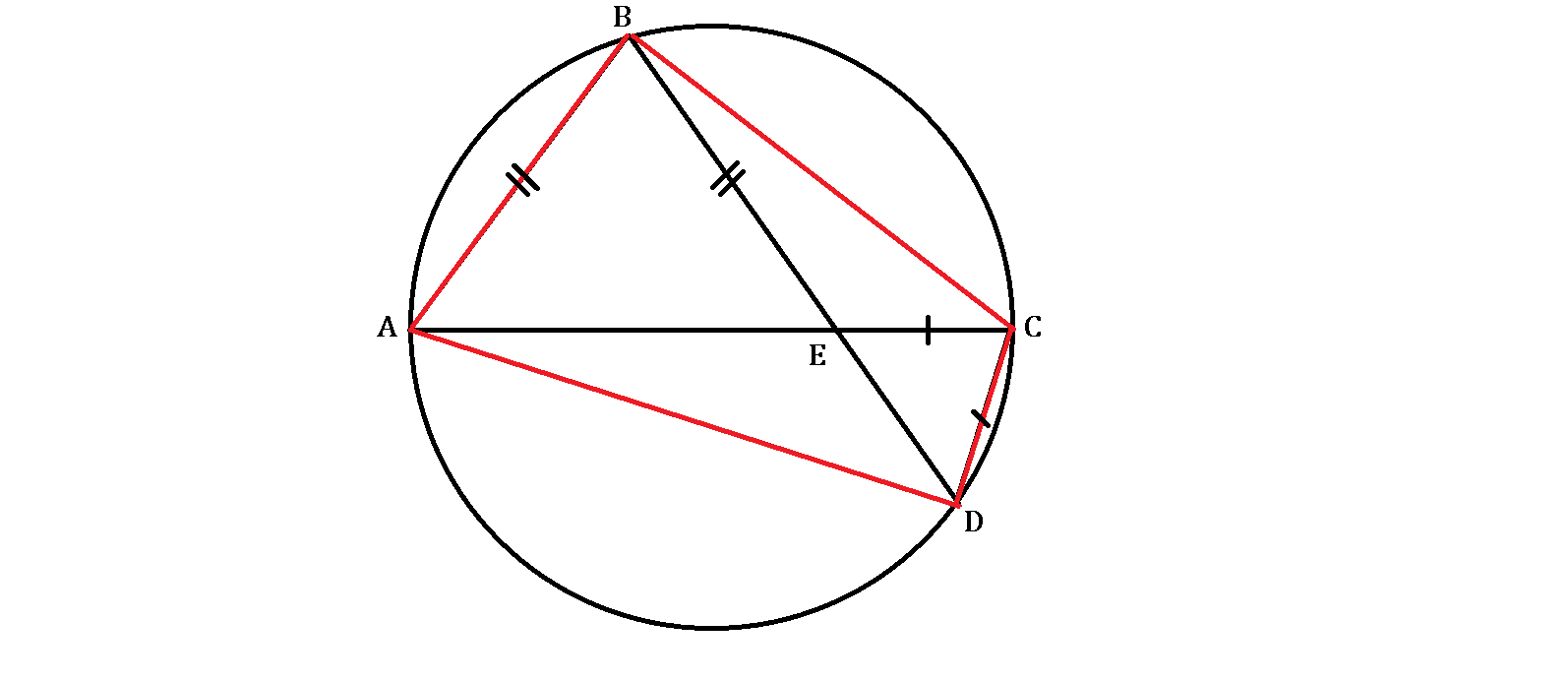
Once upon a time, Ptolemy drew a cyclic quadrilateral along with its diagonals inscribed in a circle as shown above.
Ptolemy : Thou shall see that the diagonal is indeed the diameter of the circle. It intersects another diagonal at point . Now speak to me. How magic is this point ?
Pupil : All the segments originating from this point to the vertices have the lengths in distinct integers, my master. Also, , and .
Ptolemy : Clever boy! Thus, what is the perimeter of this cyclic quadrilateral ?
The answer is 330.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the center of the circle be O , its radius r = 6 2 . 5 , ∠ A O B = θ and A B = B E = x . Since △ A B O and △ A B E are similar, ∠ A B E = ∠ A O B = θ . Because A B C D is a cyclic quadrilateral the diagonal angles ∠ A B D = ∠ A C D = θ . Therefore △ A O B , △ A B E , and △ C D E are similar isosceles triangles.
Then A B A E = A O A B ⟹ A E = r x 2 . And E C E D = 2 r − A E E D = r x ⟹ E D = 2 x − r 2 x 3 . Since B D = B E + E D = 3 x − r 2 x 3 = 1 1 7 ⟹ 4 x 3 − 4 6 8 7 5 x + 1 8 2 8 1 2 5 = 0 . Solving the equation, we get x = A B = 7 5 . C D = x r × D E = 7 5 6 2 . 5 ( 1 1 7 − 7 5 ) = 3 5 . B C = 1 2 5 2 − 7 5 2 = 1 0 0 , and D A = 1 2 5 2 − 3 5 2 = 1 2 0 .
Therefore, the perimeter of A B C D is A B + B C + C D + D A = 7 5 + 1 0 0 + 3 5 + 1 2 0 = 3 3 0 .