Pull it, Mr Pulley!
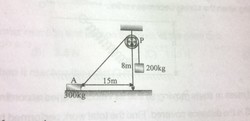 Find the velocity of A in the figure after it has started from rest in the position shown and travelled 9m along the frictionless surface.
Find the velocity of A in the figure after it has started from rest in the position shown and travelled 9m along the frictionless surface.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Relevant wiki: Conservation of Energy
The change in height of block B is 1 5 2 + 8 2 − ( 1 5 − 9 ) 2 + 8 2 = 1 7 − 1 0 = 7 ⇒ Δ h = 7
Conservation of Energy gives, T a + T b = Δ U b
Taking constraint relations, s a 2 = s b 2 + h 2
Differentiating, 2 s a d s a = 2 s b d s b d t d s a = s a s b d t d s b = sin θ d t d s b v a = v b sin θ ⋯ ( 1 )
Hence conserving energy, 2 1 m a v a 2 + 2 1 m b v b 2 = m b g Δ h
Using ( 1 ) , ⇒ v a 2 ( m a + m b sin 2 θ ) = 2 m b g Δ h v a = m a + m b sin 2 θ 2 m b g Δ h
Substituting values, v a = 8 . 5 8 8 5 6
Thanks to Deeparaj Bhat for an excellent explanation.