Pull up the Gun
Probability
Level
3
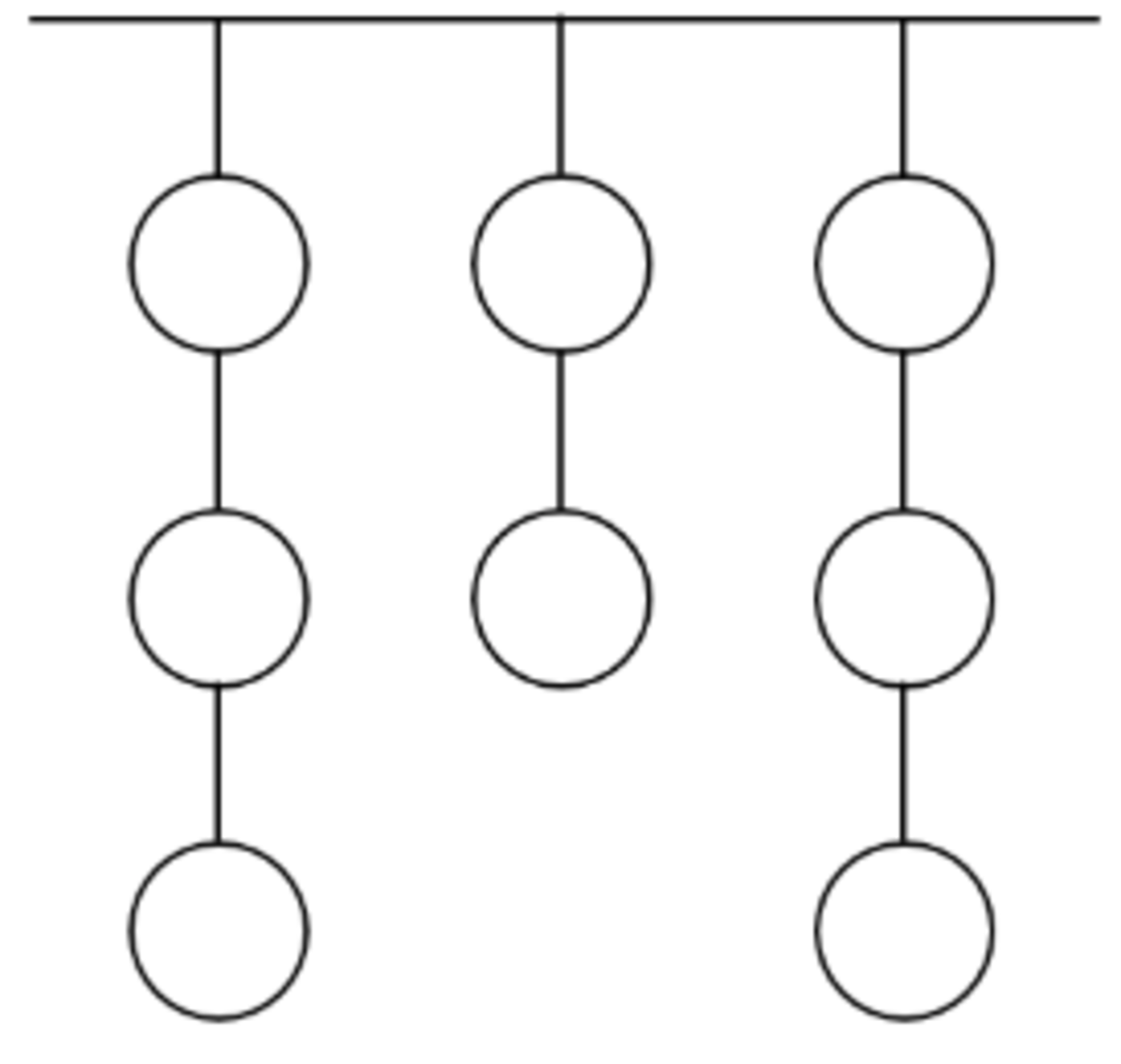
Eight clay targets are arranged as shown above. In how many different orders can these targets be shot if no target can be shot unless the one below it has been shot?
The answer is 560.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
There are 8 ! ways to shoot the targets, ignoring the rule.
There are 3 ! , 2 ! , 3 ! ways for the relative order of shooting the targets in each column, but only 1 order is valid, per the rules.
Thus, the number of valid orders is 3 ! × 2 ! × 3 ! 8 ! = 5 6 0 .
Remark: Another way of thinking about this is to label the targets A 1 , A 2 , A 3 , B 1 , B 2 , C 1 , C 2 , C 3 and make a similar argument about the number of words you can form if the A i are indistinguishable; in other words, it is the number of distinct words than can be made with 3 As, 2 Bs, and 3 Cs.