Pull
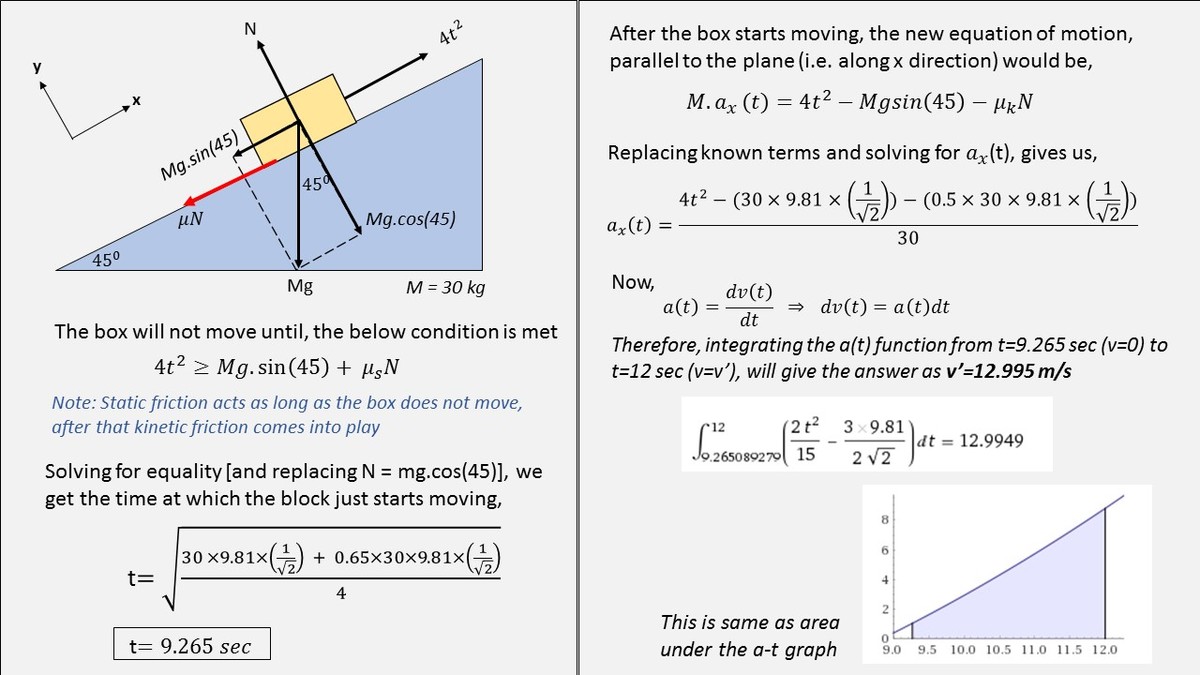
An electric motor pulls a 30kg box up an incline elevated 45 degrees with a force F = 4 t 2 parallel to the incline. If the system starts at rest with the box at the bottom of the incline, and the coefficient of static friction is μ s = 0 . 6 5 and the coefficient of kinetic friction is μ k = 0 . 5 , then how fast is the box going at 12 seconds?
Use g = 9 . 8 1 s 2 m .
The answer is 12.995.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
First we need to find when the box starts moving. So we sum the forces along the incline, with the direction up the incline as being positive, it will start moving the instant after the forces balance. ↗ + ∑ F i n c : ↗ + ∑ F i n c : 0 = 4 t 2 − m g ( sin θ + μ s cos θ ) t = 4 m g ( sin θ + μ s cos θ ) . Entering the numbers for this question gives t = 9 . 2 6 5 s . We know that the net force up the ramp is impulsive, so the following relationship holds m v 1 + ∫ t 1 t 2 ∑ F d t = m v 2 m 1 ∫ t 1 t 2 4 t 2 − m g ( sin θ + μ k cos θ ) d t = v 2 and plugging in the values in the problem, and t 1 = 9 . 2 6 5 gives v 2 = 1 2 . 9 9 5 2 m .
We have to start by making an important realization: the block won't start moving until the force being applied is greater than the sum of the parallel force and static frictional force opposing the block's motion. Thus, we need to first find the time t 0 at which the applied force and the resistive forces are equal:
F a = F ∣ ∣ + F s ⇒ 4 t 0 2 = m g sin θ + m g cos θ μ s ⇒ t 0 = 4 m g ( sin θ + μ s cos θ ) = 4 ( 3 0 ) ( 9 . 8 1 ) ( sin 4 5 ∘ + 0 . 6 5 cos 4 5 ∘ ) ≈ 9 . 2 6 5 s
Now, we must find the net force acting on the block once it has started to move:
F = m x ¨ = 4 t 2 − m g ( sin θ + μ k cos θ ) ⇒ x ¨ = m 4 t 2 − g ( sin θ + μ k cos θ )
Now we have to integrate the acceleration to get the function for velocity. We set the bounds of integration to an upper bound of 1 2 , as we want to find out how fast the box is going at 1 2 seconds, and the lower bound of t 0 , as this is the time at which the box begins to move, therefore x ˙ ( t 0 ) = 0 :
∫ t 0 1 2 x ¨ dt = x ˙ ( 1 2 ) − x ˙ ( t 0 ) = x ˙ ( 1 2 )
⇒ x ˙ ( 1 2 ) = ∫ t 0 1 2 ( m 4 t 2 − g ( sin θ + μ k cos θ ) ) dt = ∫ t 0 1 2 m 4 t 2 dt − g ( sin θ + μ k cos θ ) ∫ t 0 1 2 dt
⇒ 3 m 4 t 3 − g ( sin θ + μ k cos θ ) t ∣ ∣ ∣ ∣ t 0 1 2 = 3 ( 3 0 ) 4 t 3 − ( 9 . 8 1 ) ( sin 4 5 ∘ + 0 . 5 cos 4 5 ∘ ) t ∣ ∣ ∣ ∣ 9 . 2 6 5 1 2 ≈ 1 2 . 9 9 5 m / s 2