Pulley Dynamics in Horizontal plane
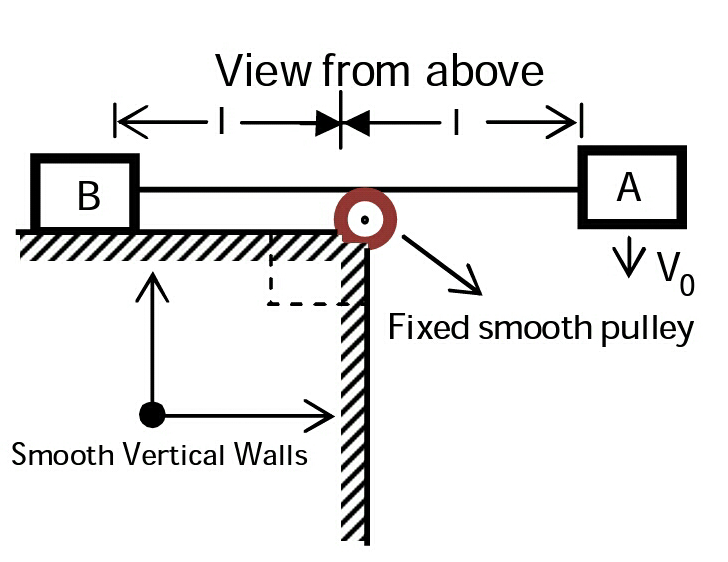 Two identical blocks are placed on a smooth horizontal surface connected by a light string of length
2
l
. String touches a fixed smooth pulley at its mid point initially. Shaded parts are two smooth vertical walls.
Two identical blocks are placed on a smooth horizontal surface connected by a light string of length
2
l
. String touches a fixed smooth pulley at its mid point initially. Shaded parts are two smooth vertical walls.
Block A is given a velocity v perpendicular to string as shown in diagram at time t = 0 . Block B strikes the pulley and stops.
Find the time t when block A hits the wall. If t = v l ( a + 2 π ( 1 − d b c ) ) , find the value of a + b + c + d .
ORIGINAL
Image Credit: AITS
The answer is 13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
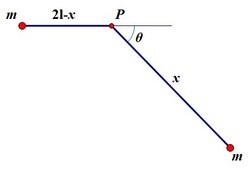 While block
B
has not yet hit the pulley, let
x
be the distance of block
A
from the pulley, and let
T
be the tension in the string. The only force acting on
A
is central, so the angular momentum of
A
is conserved during this motion, so that
x
2
θ
˙
=
ℓ
v
. We also have the radial equation of motion
m
(
x
¨
−
x
θ
˙
2
)
=
−
T
while the equation of motion of
B
is simply
m
x
¨
=
T
and hence
2
x
¨
−
ℓ
2
v
2
x
−
3
=
0
The usual change of variable
u
=
x
−
1
yields
x
˙
=
−
ℓ
v
d
θ
d
u
and
2
d
θ
2
d
2
u
+
u
=
0
and hence (since
u
=
ℓ
−
1
and
d
θ
d
u
=
0
when
θ
=
0
) we have
u
=
ℓ
1
cos
(
2
θ
)
This stage of the motion lasts until
x
=
2
ℓ
, which happens when
cos
(
2
θ
)
=
2
1
, so when
θ
=
3
2
π
. During this motion
θ
˙
=
ℓ
v
x
−
2
=
ℓ
v
u
2
=
ℓ
v
cos
2
(
2
θ
)
so that the first stage of the motion lasts for time
t
1
, where
t
1
=
v
ℓ
∫
0
3
2
π
sec
2
(
2
θ
)
d
θ
=
v
ℓ
6
For the second stage of the motion (since
(
2
ℓ
)
2
θ
˙
=
v
ℓ
), particle
A
moves in a circular arc of radius
2
ℓ
with constant angular velocity
4
ℓ
v
, and so the additional time until particle
A
hits the wall is
t
2
=
v
4
ℓ
(
2
1
π
−
3
2
π
)
=
v
2
π
ℓ
(
1
−
3
2
2
)
making the required total time
t
1
+
t
2
=
v
ℓ
(
6
+
2
π
(
1
−
3
2
2
)
)
which makes the answer
6
+
2
+
2
+
3
=
1
3
.
While block
B
has not yet hit the pulley, let
x
be the distance of block
A
from the pulley, and let
T
be the tension in the string. The only force acting on
A
is central, so the angular momentum of
A
is conserved during this motion, so that
x
2
θ
˙
=
ℓ
v
. We also have the radial equation of motion
m
(
x
¨
−
x
θ
˙
2
)
=
−
T
while the equation of motion of
B
is simply
m
x
¨
=
T
and hence
2
x
¨
−
ℓ
2
v
2
x
−
3
=
0
The usual change of variable
u
=
x
−
1
yields
x
˙
=
−
ℓ
v
d
θ
d
u
and
2
d
θ
2
d
2
u
+
u
=
0
and hence (since
u
=
ℓ
−
1
and
d
θ
d
u
=
0
when
θ
=
0
) we have
u
=
ℓ
1
cos
(
2
θ
)
This stage of the motion lasts until
x
=
2
ℓ
, which happens when
cos
(
2
θ
)
=
2
1
, so when
θ
=
3
2
π
. During this motion
θ
˙
=
ℓ
v
x
−
2
=
ℓ
v
u
2
=
ℓ
v
cos
2
(
2
θ
)
so that the first stage of the motion lasts for time
t
1
, where
t
1
=
v
ℓ
∫
0
3
2
π
sec
2
(
2
θ
)
d
θ
=
v
ℓ
6
For the second stage of the motion (since
(
2
ℓ
)
2
θ
˙
=
v
ℓ
), particle
A
moves in a circular arc of radius
2
ℓ
with constant angular velocity
4
ℓ
v
, and so the additional time until particle
A
hits the wall is
t
2
=
v
4
ℓ
(
2
1
π
−
3
2
π
)
=
v
2
π
ℓ
(
1
−
3
2
2
)
making the required total time
t
1
+
t
2
=
v
ℓ
(
6
+
2
π
(
1
−
3
2
2
)
)
which makes the answer
6
+
2
+
2
+
3
=
1
3
.
neglect gravity
Log in to reply
Since all motion takes place on a smooth horizontal surface, gravity has no bearing on the problem.
on falling block if gravity acts about pulley you cannot conserve angular momentum
Log in to reply
The block is not falling. As I have already said, the motion is taking place on a horizontal plane. Imagine looking at the blocks on a smooth table top from above.
i understood now
Another solution is by using energy instead of force equations
Log in to reply
@Kushal Thaman How can you introduce time in the question using only energy conservation. Please post your solution?
@Legend of Physics credits to a friend for the solution who wrote it, but how do I attach a pic of his solution in the comments box?
Log in to reply
@Kushal Thaman From brilliant Website go to any question solution which you have solved correctly. There will be an option of photo . Generate that link and copy it to here and delete it from that different question solution.
Can you please explain why block Bwill strike the pulley first. Also in the 6th line it should be VX INSTEAD OF VY
Log in to reply
It is well known that B strikes first, see Krotov for more details.
can someone please do using energy method i dont think i agree with angular momentum equations
