Pulley From The Other World
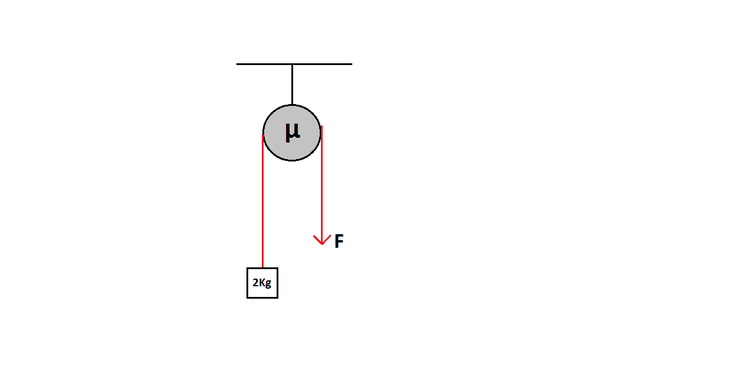 A block of mass
2
kg
is to be lifted with constant velocity by applying force
F
down the rope that passes over a pulley having coefficient of friction
μ
w.r.t. the rope. If the pull required for this (in Newtons) is
X
, evaluate
⌊
X
⌋
.
A block of mass
2
kg
is to be lifted with constant velocity by applying force
F
down the rope that passes over a pulley having coefficient of friction
μ
w.r.t. the rope. If the pull required for this (in Newtons) is
X
, evaluate
⌊
X
⌋
.
Details and Assumptions
1) The pulley and rope are massless.
2)
μ
=
2
3) Take
g
=
1
0
m
s
−
1
.
4) The force is applied vertically downwards.
5)
⌊
.
⌋
denotes the Greatest Integer Function.
The answer is 10709.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Wow!What a solution. It is really very elegant. I admire you a lot. @Deepanshu Gupta
The relation between tension at the slag and tight sides is given below where the angle of lap is in radians, here it is
π
.
T
t
=
e
μ
∗
π
∗
T
s
This is well known relation that Deepanshu Gupta has proved.
Log in to reply
Exactly, it is very well known. Is it taught in engineering courses,sir?
Log in to reply
It is the well known Capstan Equation Relating tensions across a rope on a pulley having friction
- This problem is incorrectly worded. A "pulley" is a wheel on an axle that can rotate. Here the rope passes over a fixed cylinder.
- It does not make any sense to specify a coefficient of friction as large as 2. It makes the "correct" answer utterly un-physical.
- It does not make any sense to expect the numerical answer to be correct to five significant digits, especially when you use g=10m/s^2.
Log in to reply
Whilst the theory is right, you have injected some common sense in to this problem. Thank you. The principal is right, though. Two loops around almost any fixed cylinder is as good tied in place.
This problem has been derived from Problem 2.24 of Introduction to Mechanics by Kleppner and Kolenkow. While I was suspecting this method will be used , I didn't try it because the answer was too large.
This is a very very sticky pulley, essentially it is a stuck fast. Values of CoF for a polypropylene rope over polished (if it does start that would become so soon!) steel would be much less than 1.
Yeah I did it the same way Excellent qn...
THIS ANALYSIS IS FALSE BECUASE : 1-WE NEED TO LIFT 20 N BY FORCE = 10709.3N IS TO MUCH. 2-THERE IS NO SENSE IN THIS ANALYSIS RESULT.
Log in to reply
No, it is correct since we are also taking into account the friction between pulley and string.
Try to prove
X = m g × e π μ
μ - frictinal coefficient
can anyone give a full solution @krishna sharma
Log in to reply
I uploaded that! You may refer to that @Mardokay Mosazghi
only thing bothering me is the angle, i think it would be slightly less than pi and we cannot neglect it since it varies exponentially .
Really This is an Interesting question ! @Ishan Singh create very good question Finally I'm able to solved This question after a wrong attempt .
See Following Images first carefully !
Since small rope element which we consider is in equilibrium ( Moving with constant velocity ) So we Balanced Forces in X and Y direction Respectively.
X-axis :
( T + d T ) cos ( 2 d θ ) = T cos ( 2 d θ ) + d f n e t ∵ cos ( 2 d θ ) ≈ 1 ⇒ d T = d f n e t . . . ( 1 ) .
Y-axis :
T sin 2 d θ + ( T + d T ) sin 2 d θ = N ∵ sin 2 d θ ≈ 2 d θ ⇒ T d θ + d T ( 2 d θ ) = N ∵ d T ( 2 d θ ) ≈ 0 ⇒ T d θ = N . . . . ( 2 ) .
Also
d f n e t = μ N . . . . ( 3 ) .
using all 3 equations we get relation :
T d T = μ d θ ∫ m g F T d T = μ ∫ 0 π d θ F = m g × e π μ = 1 0 7 0 9 . 3 Q . E . D .