Pulley Logic by Fernando da Vinci
Fernando da Vinci, one of the famed Leonardo’s many and little-known half-brothers, has left behind drawings of ingenious mechanisms involving pulleys, ropes, and springs. Historians and engineers were able to recreate his drawings using modern notation and translated into English, as shown as in this graphic, showing 7 distinct and separate mechanisms and their frames.
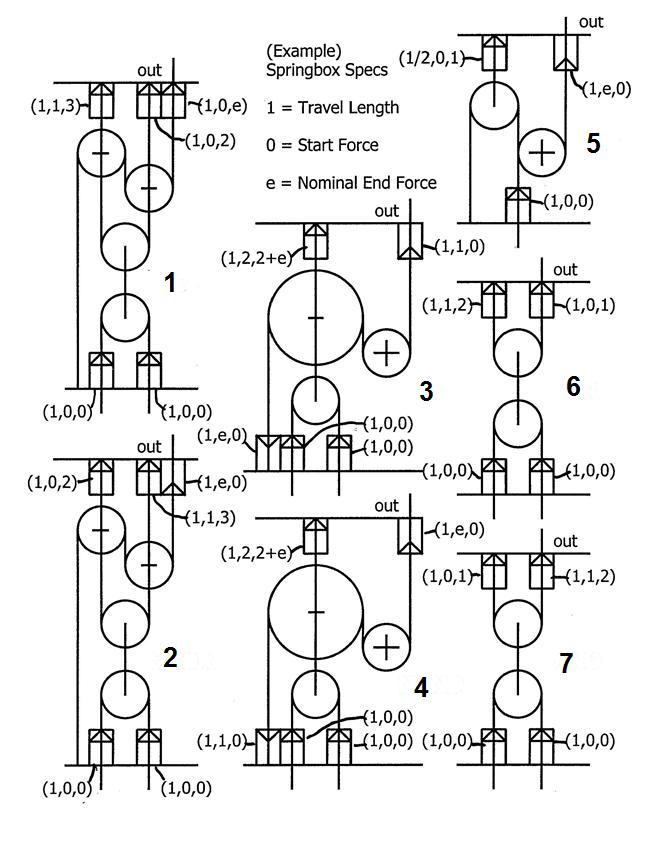 They realize now that entirely by pulley, rope and spring action, these mechanisms functioned as logic gates! Four centuries before digital computers! But they first had to figure out and make the following assumptions:
They realize now that entirely by pulley, rope and spring action, these mechanisms functioned as logic gates! Four centuries before digital computers! But they first had to figure out and make the following assumptions:
Pulleys
Circles of radii and represent pulley wheels. A + sign in the center of a circle indicates that the pulley’s axle is fixed in the frame space. A vertical line terminating in the center of a center indicates that the pulley’s axle is tethered to the end of a rope but otherwise free to move with the rope. A – sign in the center of a circle with a vertical line running through it indicates that the pulley’s axle is tethered to the length of a rope at that point, but likewise otherwise free to move with the rope.
Ropes
Vertical lines represent flexible ropes, which may be 1) fixed to the frame, 2) tethered to the axle of a pulley wheel, 3) fixed to the end of a spring in a spring cage, or 4) passing either through the frame from the bottom or through the top of the frame. Where the diagrams suggests, ropes may pass around a pulley wheel, and in figure in particular, ropes pass around the top pulley wheel, one terminating in a spring cage at the bottom of the frame, the other passing around the pulley that has a fixed axle.
Spring Cages
Small rectangular boxes with arrows inside represent a spring assembly, through the center of which passes a rope. The rope is attached to the spring where the arrows are, and such arrows are free to move, constrained by the force of the spring. The arrows indicate the direction of the spring force. The travel of the arrow (and the rope affixed to it) is limited by the length of the spring cage. If the arrow is shown “sitting at the bottom of a spring cage”, it indicates that tension in the rope is already pulling the arrow down to the limit of its travel in the spring cage, in the initial state of that assembly of pulleys, ropes, and spring cages
Spring Forces in Cages
Each spring cage has characteristics which is represented by a tuple , where
a
indicates the maximum length of travel of the arrow
b
indicates spring force in the initial position, in the arrow’s direction
c
indicates spring force in the final position, after maximum travel of the arrow
A tuple of means there’s no spring, even though travel is still limited. A value of means a nominal figure .
Input and Output
The rope(s) passing through the bottom of the frame represents the input(s), while the rope passing through the top of the frame (where marked as “out”) represents the output. All input and output rope travel length is limited to , and they are either in the down position, representing the 1 logic state, or they are in the up position, representing the 0 logic state. If the output rope travels from up to down position, then it has gone from logic state 0 to logic state 1 , and likewise if it travels from down to up position, then it has gone from logic state 1 to logic state 0 . It is assumed that there will always be some nominal tension on the output rope.
Given the following list of logic gates in order from through
1)
NOT
2)
AND
3)
OR
4)
XOR
5)
NAND
6)
NOR
7)
XNOR
list the Figure numbers of the mechanisms which function correspond with these logic gates in the same order, and give your answer as a digit number.
See Logic Gates
Note
Coiled springs first appeared as early as 15th century
Also, this is a made up story but the problem is still real
The answer is 5761432.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The rope in the spring cage with the greatest initial directional force (compared to its opposing end) does one of two things;
Moves in the direction of its force first,
Or moves away from the direction of its force last.
5 7 6 1 4 3 2