Pulley Pan

Classical Mechanics Level 2

A block of mass $m$ is connected to a pan of mass $m$ as well over a pulley system with negligible mass and friction. The system is at rest initially, however, a ball of mass $m$ falls down on it. If the velocity of the ball right before the moment of collision is $v$ , then what is the velocity of the system right after the collision.

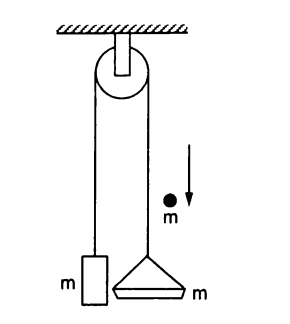
Details and Assumptions

Let the collision between the pan and the ball be completely inelastic.
Let the final velocity of the ball be $15$ $m/s$ .
Assume that the rope and the pulley have negligible mass and no friction at all.
Answer with two significant digits.

The answer is 5.0.

1 solution

Raghu Alluri
Mar 24, 2019

This is a simple problem which can be solved in many different ways such as using impulse. However, we will use simple algebra to solve it by using the conservation of momentum. For this, the system must be defined and it should include the Earth, the hanging mass, the pan and of course the ball.

This way the momentum will be conserved. The conservation in this situation can be expressed as the following,

$mv_b + 2mv_{sys i} = (m + 2m)v_{sys f}$

Thus we get,

$mv_b = 3mv_{sysf}$

$v_{sysf} = mv / 3m = v / 3$

Therefore, we can conclude that the velocity of the system will be exactly a third of the final velocity of the ball. Conceptually this makes sense because they all have the same mass and thus if momentum was conserved the velocity of the whole system would be one-third of the value of any one of the final velocities.

So if the velocity of the ball was given to be $15$ $m / s$ then,

$v_{sysf} = v / 3 = 15 / 3 = 5.0$

Therefore,

$v_{sysf} = 5.0$ $m / s$

Pulley Pan

The answer is 5.0.

1 solution

0 pending reports