Pulley System, Stop Spring,Sliding Crate w/ Friction

Classical Mechanics Level 4

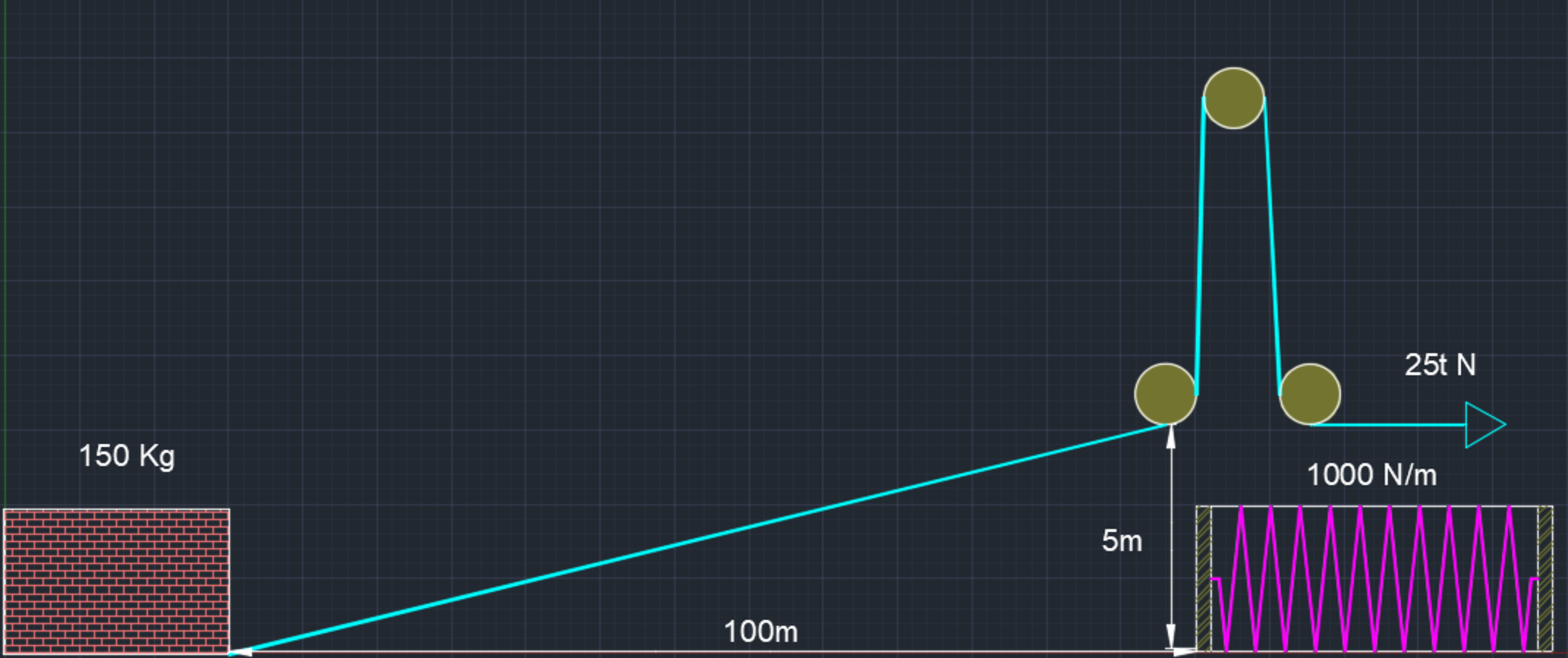A motor is attached to a cable that pulls a crate loaded with bricks toward a spring stopping mechanism. The force exerted is F(t)=25t N. The crate of bricks has a mass of 150 Kg. The spring stiffness k=1000 N/m. The coefficient of static friction is 0.70. The coefficient of kinetic friction is 0.45. At a time 6.5 seconds after motion begins the motor shuts off and the crate slides toward the spring. Find the distance from the spring where the crate comes to rest. Note: g=9.81 m/s^2 and there is no friction beneath the spring.


The answer is 0.304.

A Former Brilliant Member by A Former Brilliant Member

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Steven Chase
Mar 24, 2020

Nice problem. It is solved in multiple stages, with each stage having its own comments. 

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
 
import math

# Constants

h = 5.0

m = 150.0
k = 1000.0
us = 0.7
uk = 0.45
g = 9.81

dt = 10.0**(-5.0)

print "height"
print h
print ""

####################################################################

# Determine the time at which the block starts moving
# This is when the horizontal pull exceeds .....
# ... the product of the static friction coeff and the upward normal force
# (Fx,Fy) are the pulling forces from the cable

t = 0.0

theta = math.atan(h/100.0)

Fx = 0.0
N = m*g

while Fx <= us*N:

    F = 25.0*t

    Fx = F*math.cos(theta)
    Fy = F*math.sin(theta)

    N = m*g - Fy

    t = t + dt

print "tstart"
print t
print ""

####################################################################

# Calculate the block motion until 6.5 seconds after starting
# ...when the motor stops pulling
# x corresponds to the location of the block (treated as a point particle)

tstop = t + 6.5 

x = 0.0
xd = 0.0
xdd = 0.0

while t <= tstop:

    x = x + xd*dt
    xd = xd + xdd*dt

    theta = math.atan(h/(100.0-x))

    F = 25.0*t

    Fx = F*math.cos(theta)
    Fy = F*math.sin(theta)

    N = m*g - Fy

    Fxnet = Fx - uk*N

    xdd = Fxnet/m

    t = t + dt

print "x when pull stops"
print x
print ""

####################################################################

# Calculate the block motion until the block hits the spring

while x <= 100.0:

    x = x + xd * dt
    xd = xd + xdd*dt

    F = -uk*m*g

    xdd = F/m

    t = t + dt

####################################################################

# Block leaves spring with same energy it had upon impact
# Calculate the distance the block slides from the spring until stopping
# Use energy conversion

E = 0.5*m*(xd**2.0)

# E = uk*m*g * D

D = E / (uk*m*g)

print "dt"
print dt
print ""
print "Final distance from spring"
print D

####################################################################

#height
#5.0

#tstart
#39.8584400015

#x when pull stops
#58.215376686

#dt
#1e-05

#Final distance from spring
#0.304897940183

0 Helpful 0 Interesting 1 Brilliant 0 Confused

0 Helpful 0 Interesting 0 Brilliant 1 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...