Pulleys over pulleys

Classical Mechanics Level 2

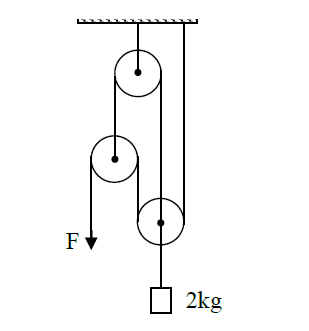What is the Force needed, in the system above, to pull the 2kg block?

10N 2N 5N 20N

1 solution

Rafael Carlini
Oct 15, 2015

We have the following schema of forces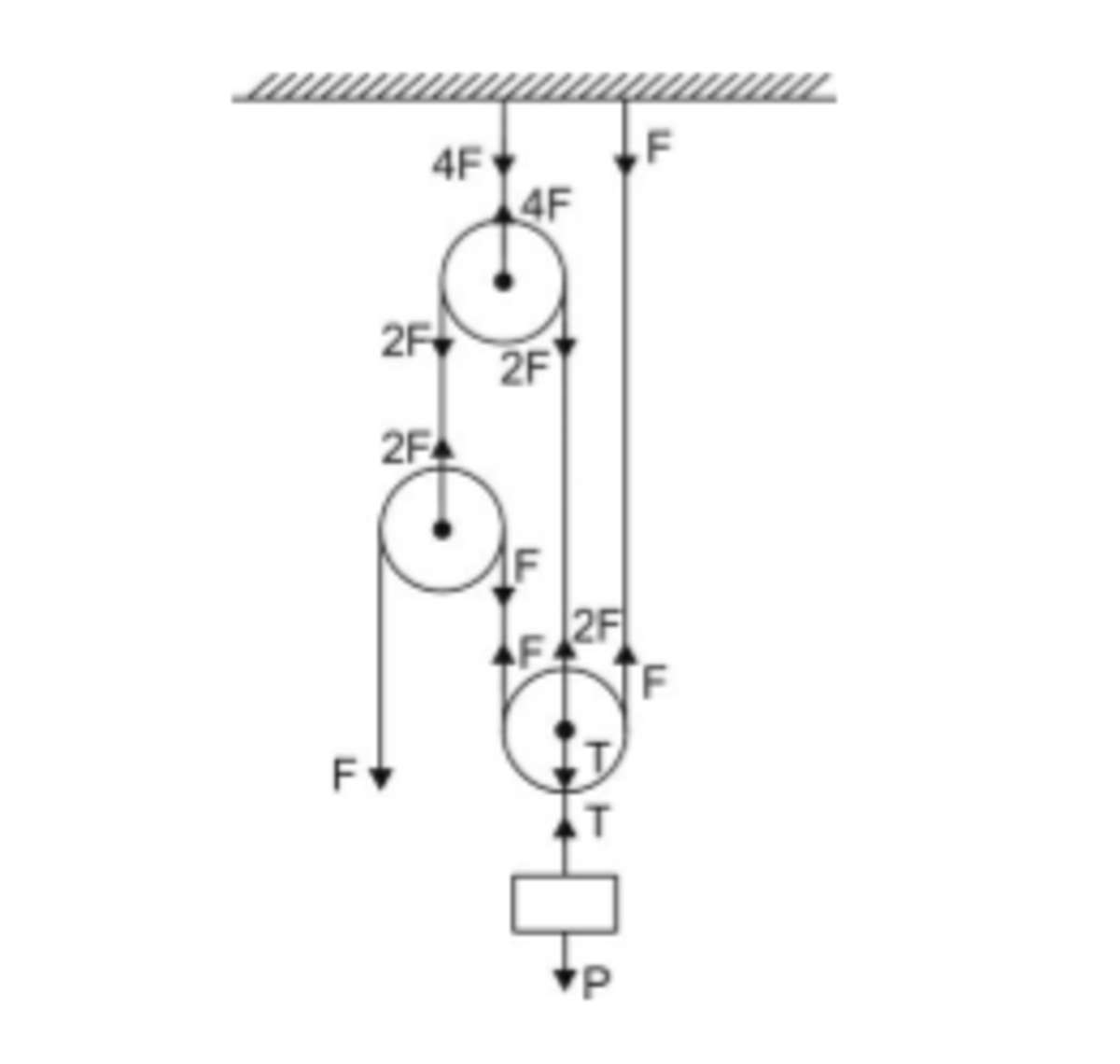

The minimum force needed to lift the block is that one necessary to bring it up in a regular speed

So, from the schema:

T = P

T = 4F

P = 4F

$2 \times 10$ = 4F

F = $\frac{20}{4}$

F = 5

We can also observe that

F = $\frac{P}{2^{n} }$

where n is the number of mobile pulleys and P is the weight of the object

is still valid in this kind of exercise.

Sorry any other English mistake, I'm from Brazil...

Half and half. Wanted to be fast. Got wrong. Actually I am trying to solve by:

W = F1 d1 = F2 d2. I thougt the second pulley is just a direction changer.

Finishing a pull of 2 L, L is lifted via one pulley with rope or string of one end fixed. Two pulleys double the half? Actually this is very imaginative until I am still not sure whether the second pulley also double the length of pull required for a lift of a length. I just believe that you are right until this moment.

I didn't think about total external force held from a pulley to tensions on two sides. I think it is only something to do with force to force or tension to tension between two sides.

If only half, then we shall not need complicated combinations. Should have chosen the right answer. Brilliant encouraged me to be fast but I think I should be careful.

Lu Chee Ket - 5 years, 7 months ago

Basically an "S" structure for doubled effects. The pulley attached on to ceiling is just a neutralizer to gravity.

Lu Chee Ket - 5 years, 7 months ago

Which one "the mobile pulley" in this system?

Mbah Abal - 5 years, 5 months ago

no ur englsh is fine, nice problem and solution ! (+1)

A Former Brilliant Member - 4 years, 6 months ago

Pulleys over pulleys

1 solution

0 pending reports