Pulleys pulleys everywhere!
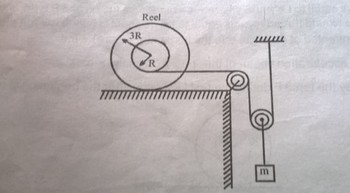 A reel has a hub radius
, the peripheral radius
and mass
. Its moment of inertia about its axis is
.
A reel has a hub radius
, the peripheral radius
and mass
. Its moment of inertia about its axis is
.
A thin massless thread is wound on a reel. A block of mass is hung through massless and frictionless pulleys as shown.
The reel is placed on a rough horizontal surface where the friction is sufficient to prevent slipping. The system is released from rest. Find acceleration to 2 decimal places (in ) of the center of mass of the reel. Take
The answer is 75.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
At any moment t , the small mass m is at height x ( t ) and velocity v ( t ) = d t d x and its kinetic energy is 2 1 m v 2 . The center of the reel must have a velocity = 3 v ( t ) giving angular velocity of ω = R v ( t ) .
The kinetic energy of the reel is 2 1 ( 4 m ) ( 3 v ) 2 + 2 3 m R 2 × ω 2 .
m . g . x ( t ) = 2 1 m v 2 + 1 8 m v 2 + 2 3 m v 2 = 2 0 m v 2 .
x ( t ) = g 2 0 . v 2 = 2 v ( t ) 2
d t d x ( t ) = 4 v ( t ) . d t d v ( t )
v ( t ) = 4 v ( t ) . a ( t )
a ( t ) = 0 . 2 5 m/s 2 = 2 5 cm/s 2 .
Acceleration of the center of the reel is 3 times the acceleration of the block, therefore,
a reel = 7 5 c m s − 2 .