Punched!
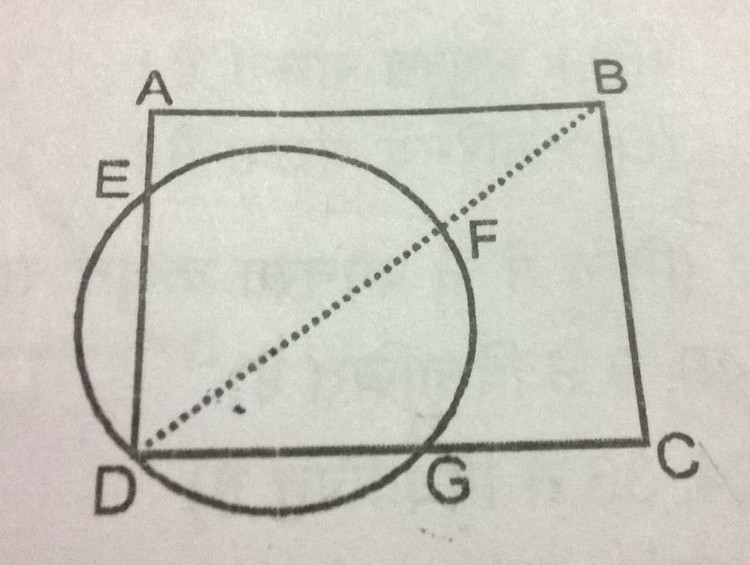 The given figure shows a square of side 8 units from which a circular hole of radius 4 units was punched using a punching machine. DF is the diameter of the hole and DFB is a striaght line. The area of the part of the circle which falls outside the sheets is (in square units):
The given figure shows a square of side 8 units from which a circular hole of radius 4 units was punched using a punching machine. DF is the diameter of the hole and DFB is a striaght line. The area of the part of the circle which falls outside the sheets is (in square units):
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
EG is the diameter of the circle as ang'DEG is 90 degrees DF & EG being diameters intersect at the center. BY completing tri angle DEG we get an isoceles one with base angles =45 degrees using this find ED =DG { ED cos45= 4} find area of triangle DEG SUBTRACT IT FROM THE AREA OF THE SEMICIRCLE AND there is the ans.......
Let's call the area we are evaluating "area A " which is composed of equal areas A 1 under the square, and A 2 to the left of the square. Let's also draw E F , F G forming areas A 3 above and A 4 to the right. Finally, let's define area B = 2 A = A 1 + A 2 + A 3 + A 4 , area C = π r 2 , and area D = s 2 , where s is the side length of square D E F G . A = 2 1 B B = C − D = 1 6 π − ( 2 8 ) 2 B = 1 6 π − 3 2 A = 8 π − 1 6
We can find the area by finding the area of the semi-circle and subtracting the area of triangle D E G .
The area of the semi-circle is just 2 1 π r 2 = 2 1 π ( 4 ) 2 = 8 π .
E G is a diameter of the circle, so E G = 8 . Since triangle D E G is a 4 5 ∘ − 4 5 ∘ − 9 0 ∘ triangle, E D = D G = 4 2 . Thus, the area of triangle D E G is 2 1 ( 4 2 ) 2 = 1 6 .
Thus, our desired area is 8 π − 1 6