"PURE" AND "NON- PURE TRIPLETS"

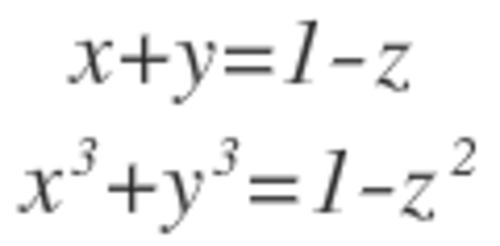If x,y,z are integers satisfying the equations given above simultaneously with the condition that sum of x and y is never zero, and if the number of ordered "PURE TRIPLETS" (x,y,z) is A and the number of ordered "NON-PURE TRIPLETS" (x,y,z) is B, then find (A+B)(A-B).

NOTE: 1. We define "PURE TRIPLETS" (x,y,z) as the ones in which ALL of x,y,z are NON-NEGATIVE INTEGERS. 2. We define "NON- PURE TRIPLETS" (x,y,z) as the ones in which x,y,z are NOT ALL non-negative integers

EXAMPLE: (9,8,7) is a "PURE TRIPLET". (-9,8,7) is a "NON-PURE TRIPLET"

NOTE: ORDERED TRIPLET means (1,2,3) IS NOT SAME AS (1,3,2) or (2,1,3) or (3,2,1).