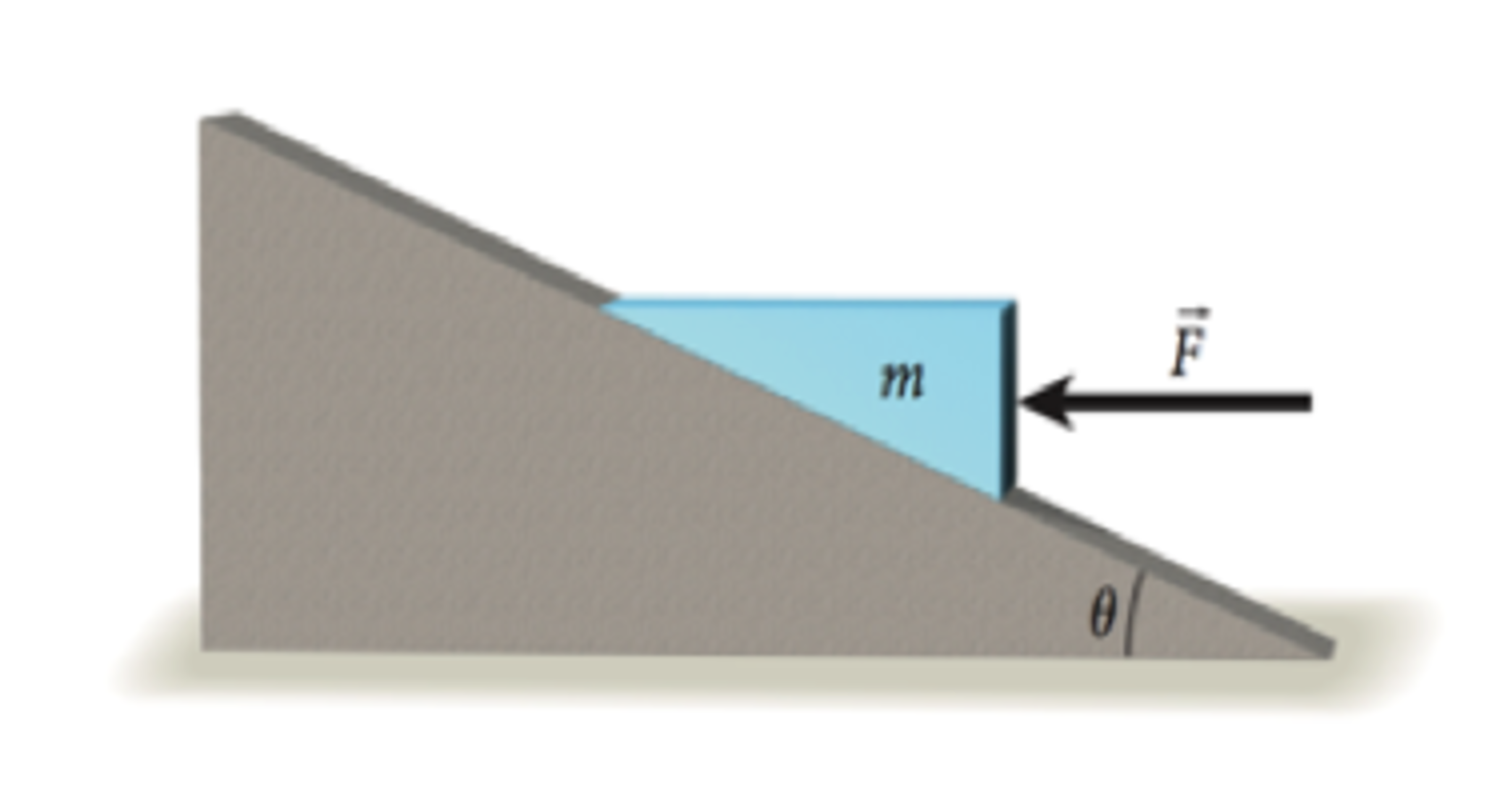
Pushing a block on a moving incline II

Classical Mechanics Level 2

A wedge of mass m 1 m_1 is located on a plane of mass m 2 m_2 that is inclined an angle θ \theta with respect to the horizontal. A horizontal force of magnitude F e x t F_{ext} pushes the wedge as shown in the figure (adapted from Bauer). The coefficient of kinetic friction between the wedge and the plane is μ 12 \mu_{12} and that between the plane and the floor is μ f l o o r \mu_{floor} . Show that the magnitude of the acceleration of the wedge with respect to the incline a 12 a_{12} and the magnitude of the incline with respect to the floor a 2 a_2 are given by:

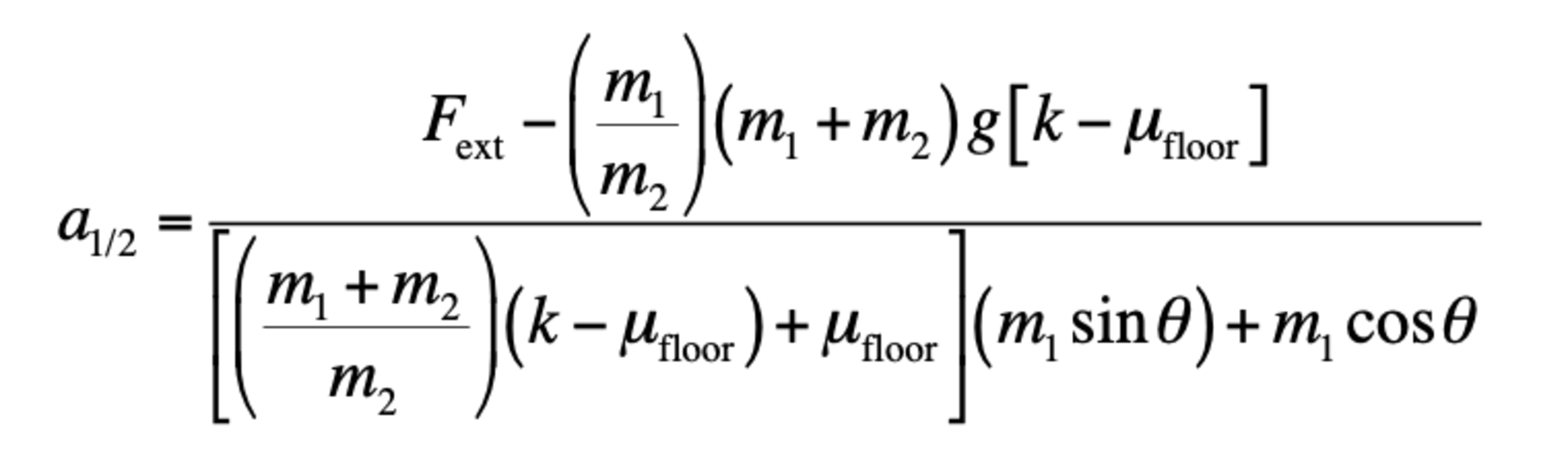
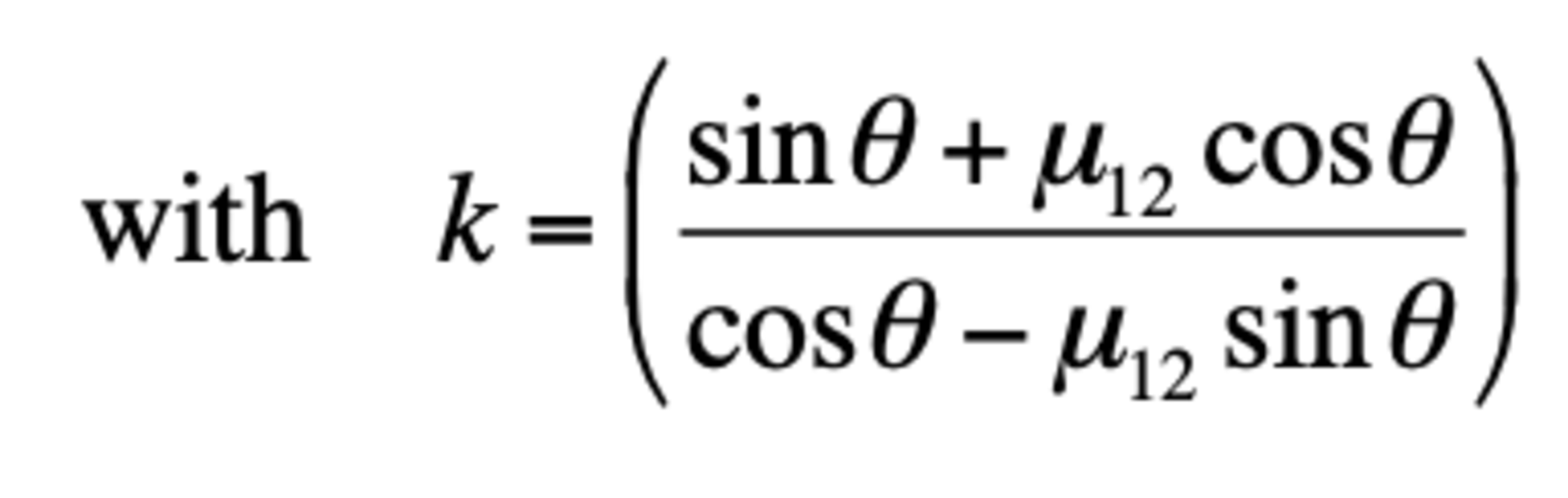
Nothing See correct answer in the problem statement

Victor Robledo-Rella by Victor Robledo-Rella , 57, Mexico

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Write down Newton 2nd law for ( x , y ) (x,y) both for the wedge and the incline. Note that the direction of motion of the acceleration of the wedge with respect to the ground is not known since the incline is also moving!... However, use the equations of relative motion to relate the acceleration of the wedge with respect to the ground in terms of the acceleration of the wedge with respect to the incline and the acceleration of the incline with respect to the ground:

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...