Pushing the boundaries: Codicil
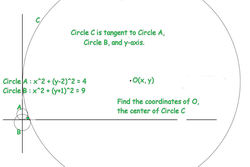 If the coordinates of O, the center of Circle C, is (x, y) find the sum x + y to the nearest 3 decimals.
If the coordinates of O, the center of Circle C, is (x, y) find the sum x + y to the nearest 3 decimals.
The answer is 55.713.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Thanks, Brian for correcting my answer.
 Graph
Graph
Log in to reply
You're welcome. :)
I'm still wrestling with "The Shrinking Square". There are no symmetries to exploit so I'm giving up on a geometric approach for now and will try some calculus later. It's a fun problem that I will re-share once I've solved it, (which is my normal process).
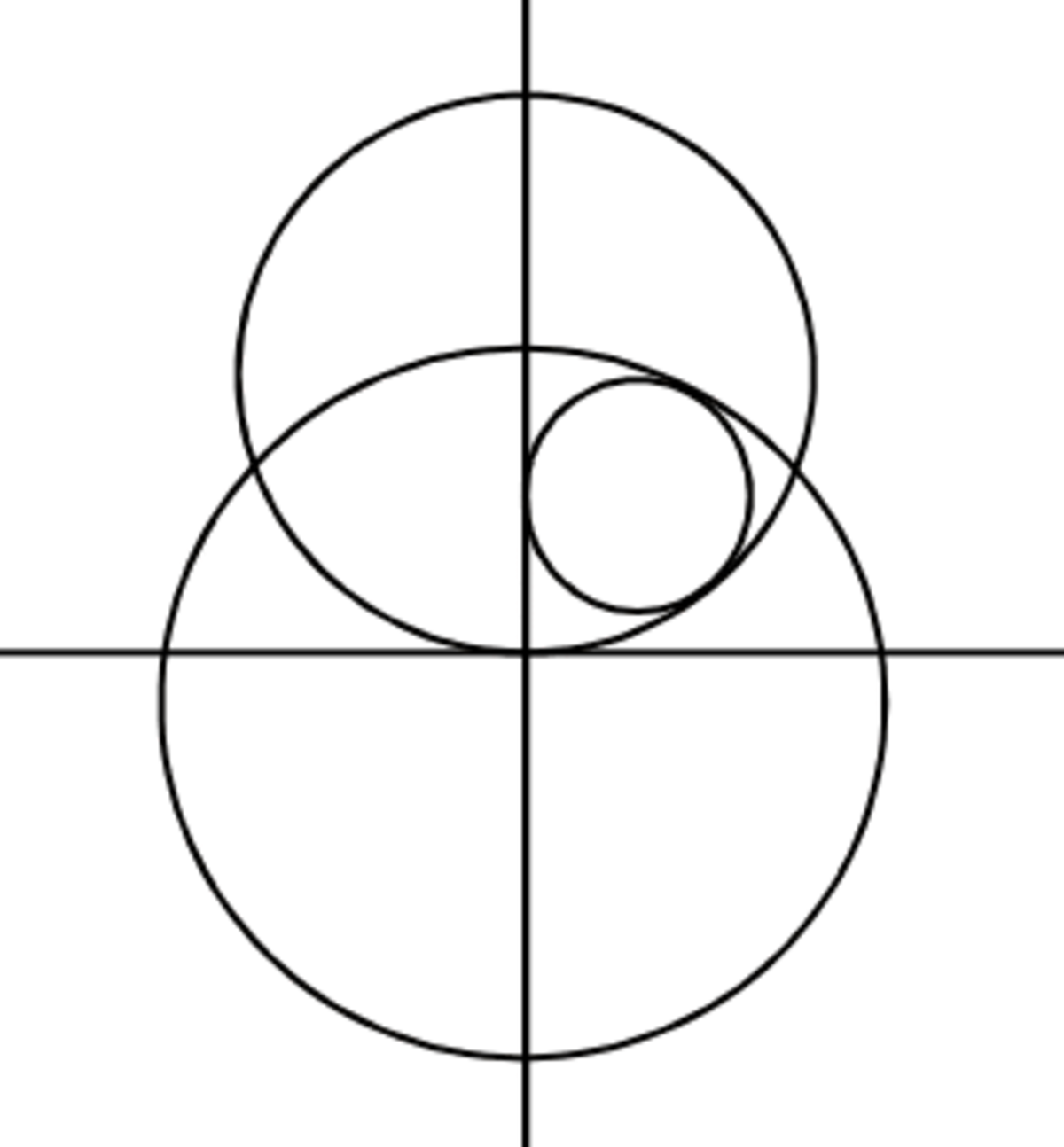
EDIT: @Guiseppi Butel Sorry to bother you again, but I'm getting a different answer than yours for "The Shrinking Square". What I ended up doing was rotating the diagram around O so that the sides of the square were aligned with the coordinate axes. This made the integration much easier, giving a value of 5 . 8 7 9 7 for the length of the side of the square, which was considered incorrect. The graph of my (rotated) solution has the corner of the square outside the circle at the top, while your "moving square" diagram would have the corner inside the circle. Maybe there are two solutions. Are our solutions close to one another?
Missed the answer because of wrong calculation--------- y 2 − 1 6 y + 1 6 = 0 , ∴ ( y − 4 ) 2 = 0 ! ! I u s e d ( y + 1 ) 2 − ( y − 2 ) 2 = ( x + 3 ) 2 − ( x + 2 ) 2 , ⟹ ( 2 y − 1 ) ∗ 3 = ( 2 x + 5 ) ∗ 1 S o 3 y = x + 4
Actually the negative solution cannot be discarded. Negative x shows up in the original equations on the right side as ( 2 − r ) 2 and ( 3 − r ) 2 respectively, where r > 0 is the radius. This is a perfectly reasonable set of equations for a circle internally tangent to both original circles.
In other words there is a second, perfectly reasonable solution. Here is how it fits in.
Since C is tangent to the y -axis its radius will be x . Let P be the point ( 0 , y ) , Q ( 0 , 2 ) be the center of circle A and S ( 0 , − 1 ) be the center of circle B .
Then Δ O P Q is a right triangle with legs length x , ( y − 2 ) and hypotenuse length ( x + 2 ) , and Δ O P S is a right triangle with legs length x , ( y + 1 ) and hypotenuse length ( x + 3 ) .
We thus have the following set of equations:
(i) x 2 + ( y − 2 ) 2 = ( x + 2 ) 2 and
(ii) x 2 + ( y + 1 ) 2 = ( x + 3 ) 2 .
After subtracting (i) from (ii) and simplifying we get x = 3 y − 4 . Now substitute this back into (i) to find that
( 3 y − 4 ) 2 + ( y − 2 ) 2 = ( 3 y − 2 ) 2 ,
which after expanding and simplifying yields
y 2 − 1 6 y + 1 6 = 0 ,
which has solutions y = 2 1 6 ± 1 6 2 − 4 ∗ 1 6 = 8 ± 4 3 .
Now y = 8 − 4 3 implies that x = 3 y − 4 = 2 0 − 1 2 3 , which is less than 0 so can be discarded. That leaves us with
y = 8 + 4 3 and thus x = 2 0 + 1 2 3 .
Thus x + y = 2 8 + 1 6 3 = 5 5 . 7 1 3 to 3 decimal places.