Putnam '69 B3
If a 1 a 2 = 1 , a 2 a 3 = 2 , a 3 a 4 = 3 ⋯ and n → ∞ lim a n + 1 a n = 1 , find ∣ a 1 ∣ .
The answer is 0.797885.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I use double factorial then convert it to standard factorial. Then calculate the limit using Stirling's formula
yeah, I posted it
My latex experience is not good. So I typed in Word and screenshot it to here. I skipped the last limit calculation because I think it's well-known.


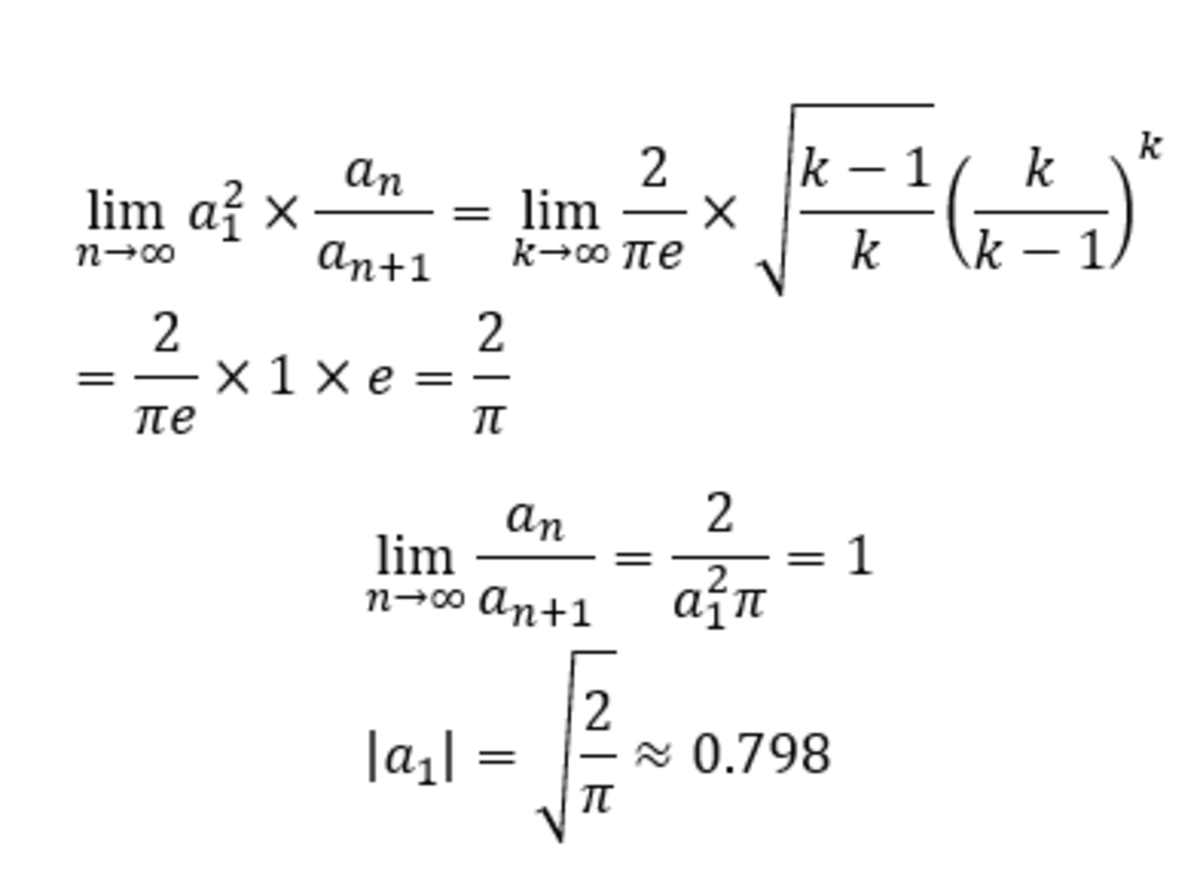
Let us substitute a few values to get an essence of the sequence -
a 2 a 3 a 4 a 5 a 6 a 7 a 8 a 9 So the general terms are a 2 n a 2 n + 1 = a 1 1 = 2 a 1 = 2 a 1 3 = 3 4 ⋅ 2 a 1 = a 1 ⋅ 2 ⋅ 4 3 ⋅ 5 = 3 ⋅ 5 a 1 ⋅ 2 ⋅ 4 ⋅ 6 = a 1 ⋅ 2 ⋅ 4 ⋅ 6 3 ⋅ 5 ⋅ 7 = 3 ⋅ 5 ⋅ 7 a 1 ⋅ 2 ⋅ 4 ⋅ 6 ⋅ 8 = a 1 ⋅ 2 ⋅ 4 ⋅ 6 ⋯ ( 2 n − 2 ) 3 ⋅ 5 ⋅ 7 ⋯ ( 2 n − 1 ) = 3 ⋅ 5 ⋅ 7 ⋯ ( 2 n − 1 ) a 1 ⋅ 2 ⋅ 4 ⋅ 6 ⋯ ( 2 n )
⟹ a 2 n + 1 a 2 n = ( a 1 ) 2 ⋅ 2 ⋅ 2 ⋅ 4 ⋅ 4 ⋅ 6 ⋯ ( 2 n − 2 ) 2 ⋅ ( 2 n ) 1 ⋅ 3 ⋅ 3 ⋅ 5 ⋅ 5 ⋯ ( 2 n − 1 ) 2
Using Wallis Product , as n → ∞
1 ⟹ a 1 = ( a 1 ) 2 1 ⋅ π 2 = π 2