Pyramid Investigations 3 – High Rise Pyramid Number
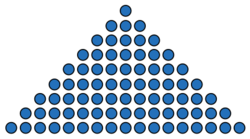 Evaluate:
Evaluate:
1 + 2 + 3 + ⋯ + 8 + 9 + 8 + ⋯ + 3 + 2 + 1 .
This problem is part of the Pyramid Investigations Set .
The answer is 81.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
31 solutions
I have another way to answer many types of this equation. Do you want to show more?
well just count the no. levels of the pyramid(n) and total no. of balls of the pryamid would be (n^2) ; here total no. of levels are 9. Therefore total no. of balls of pyramid would be 9^2 i.e. 81.
Square of the middle no. ----9 so 9^{2} =81
good
the pyramid have nine lines so 9*9=81
81
81 is correct
If you add 1+2+3+4+5+6+7+8+9+8+7+6+5+4+3+2+1=81
81
to count the balls is more easy than this equation
1+3+5+7+9+11+13+15+17=81
u can also apply the fornula Sn = [ n ( 2a + (n-1)*d ) ] /2 .
let N be the maximum integer, this problem has a closed form solution of N^2
{2 8 (8+1)/2 }+ 9
Count total rows (n) and no. of balls will be n^2
always mid term square is there here 9 so 81
81
Always adapt technical points to have more fun.........!
Easy!2(1+2+3+4+5+6+7+8)+9=2(36)+9=72+9=81
Here, n^2 is sum for all this pattern.
So 9^2=81 and mid point have 9 circle.
Count. XD Are you proud of me?
1+2+3+......+8+9+8+.....+2+1 =2(1+2+3....+8)+9 =2 8 9/2+9 =81
1+2+3+4+. . . . . +n=n*(n+1)/2
Just count the number of circles on the middle of the pyramid. Then raise it to 2: 9^2=81 So the answer is 81.
except 9 other numbers in the given sequence are given twice so 1 2+2 2+3 2+.........8 2+9=81
Sum of Natural numbers till n= n(n+1)/2.
Therefore, here, you use the above formula twice, with n=8 and then add 9 to it:
2{ 8(8+1)/2 } +9 = 81
81
I just squared the 9 in the pyramid - the largest number. The other pyramids are also similar.
I think I'm catching on...81. Where does algebra come in?
according to previous questions we learn that the series first increase then decrease when series increase and reached at maxium value after reaching maxium value he decrease simply you just take square of maxium value and in this way we get ans!!
One solution to solve this problem is that each row has a pattern (X - 2). Example: 17 + 15 (17 - 2 = 15) + 13 (15 - 2 = 13) + 11 (13 - 2 = 11) + 9 (11 - 2 = 9) + 7 (9 - 2 = 7) + 5 (7 - 2 = 5) + 3 (5 - 2 = 3) + 1 (3 - 2 = 1) = 81
Notice that:
1 + 2 + 3 + ... + n = n
(n+1)/2
Back to our equation:
1 + 2 + 3 + ... + 8 + 9 + 8 + ... + 3 + 2 + 1 = 2
(1 + 2 + 3 + ... + 8 + 9) - 9 = 9 * (9 + 1) - 9 = 9 * 9 = 81
The series can be rearranged as follows: (1+8) +(2+7 )+(3+6) +( 4+5)+(5+4)+ (6+3)+(7+2)+ (8+1)+(9) = 9x9=81
Add the numbers, starting from the bottom. As it started off with 17, it is evident that every time it moves up an roll, the number you add on decreases by 2. Continue on 'til you reach 1(the top). 17+15+13+11+9+7+5+3+1=81 Simple and stupid, yes, but the must mundane way of calculating this sum is probably this...
since we know that 1+2+3....+n+...+3+2+1= n^2 where n= no. of rows and we have 9 rows so 1+2+3...+8+9+8....+3+2+1= 9^2 = 81
last integer numbers square is the answer that is 81
Sum of !to 9 is 45, then sum of 8 to 1 is 36 ,thus total is 81 Ans
K.K.GARG,India
maximum Integer = x the sum = x² = 9² = 81
the formula of this question is n^2, so 9^9=81
(8(8+1)/2)*2+9=81 P.S==8 can be replaced by n and 9 by n+1 for a general solution
Refer to the solution of this problem which suggests that 1 + 2 + 3 + . . + ( n − 1 ) + n + ( n − 1 ) + . . . + 3 + 2 + 1 = n 2 .
Using this fact, we can solve the problem easily like this ---->
1 + 2 + 3 + . . . . . . + 8 + 9 + 8 + . . . . . + 3 + 2 + 1 = 9 2 = 8 1