Pyramid Minus Pyramid
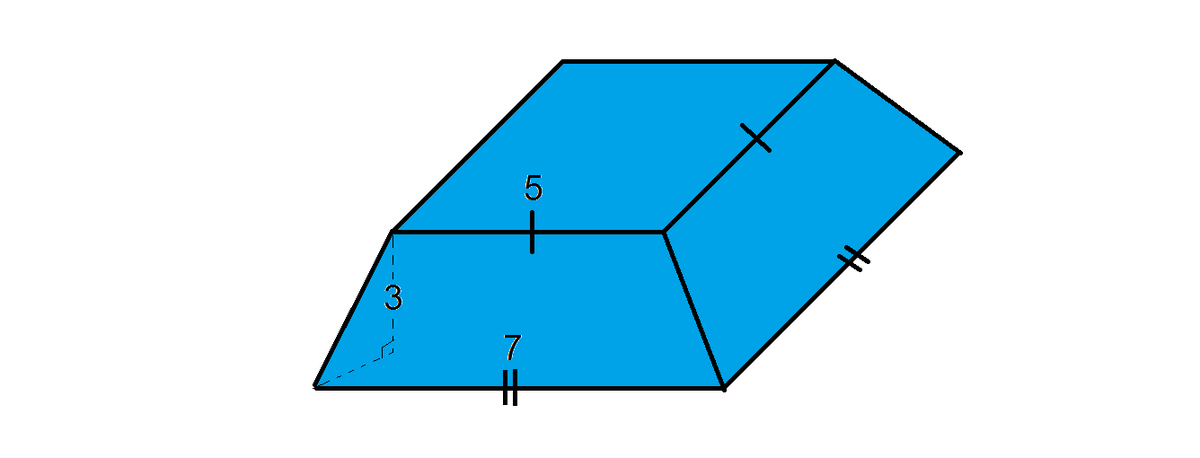
A regular pyramid of square base 7 × 7 is cut such that another regular pyramid of square base of 5 × 5 is removed, leaving a shape with the height of 3 between the parallel square planes as shown above.
What is the volume of this shape?
The answer is 109.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
The volume of the truncated pyramid = the volume of pyramid with 7 × 7 base - the volume of pyramid with 5 × 5 base.
The volume of pyramid is given by V = 3 b 2 h , where b is the side length of the base square and h , the height. For this pyramid, the relation between b and h is given by b h = 2 3 ⟹ h = 2 3 b . Therefore, V = 2 b 3 and the volume of the truncated pyramid is V t r u n c a t e d = 2 7 3 − 2 5 3 = 1 0 9 .
Suppose x be the height of the removed pyramid of square length of 5 .
Then the volume of the original pyramid = ( 3 x + 3 ) ( 7 2 ) .
On the other hand, the volume of the removed pyramid = ( 3 x ) ( 5 2 )
Thus, the solution volume = 4 9 − 3 x ( 4 9 − 2 5 ) = 4 9 + 8 x .
Then due to triangle similarity, x + 3 x = 7 5 .
7 x = 5 x + 1 5 .
x = 7 . 5
Therefore, the solution volume = 4 9 + 6 0 = 1 0 9 .
Note : the formula for the cut pyramid's volume V with upper square base length a , bigger square base length b , and height h between the planes can be generalized as:
V = 3 h ( a 2 + a b + b 2 )
The solid is in the shape of a Frustum of a Regular Pyramid and the formula for the volume is
V = 3 h ( A 1 + A 2 + A 1 × A 2 ) where A 1 and A 2 are area of the bases
Solving for A 1 we have,
A 1 = 7 × 7 = 4 9
Solving for A 2 , we have
A 2 = 5 × 5 = 2 5
Substituting, we obtain
V = 3 h ( 4 9 + 2 5 + 4 9 × 2 5 ) = 1 0 9
The volume of a frustum of a regular pyramid is given by the formula:
V = 3 ( A 1 + A 2 + A 1 × A 2 ) ( h ) where: A 1 and A 2 are area of the bases and h = height
A 1 = 5 × 5 = 2 5 ; A 2 = 7 × 7 = 4 9
Substituting, we get
V = 3 ( 2 5 + 4 9 + 2 5 × 4 9 ) ( 3 ) = 7 4 + 3 5 = 1 0 9