Pyramid Selling

Algebra Level 4

You are starting a direct-sale network with inviting $2$ friends as your first members, who will each find $2$ new members on their own. However, in order to be honored as new duo members, they must be invited and enrolled by the same person on top. In other words, the top member may not simply invite one person into the group; two newcomers are required for such membership.

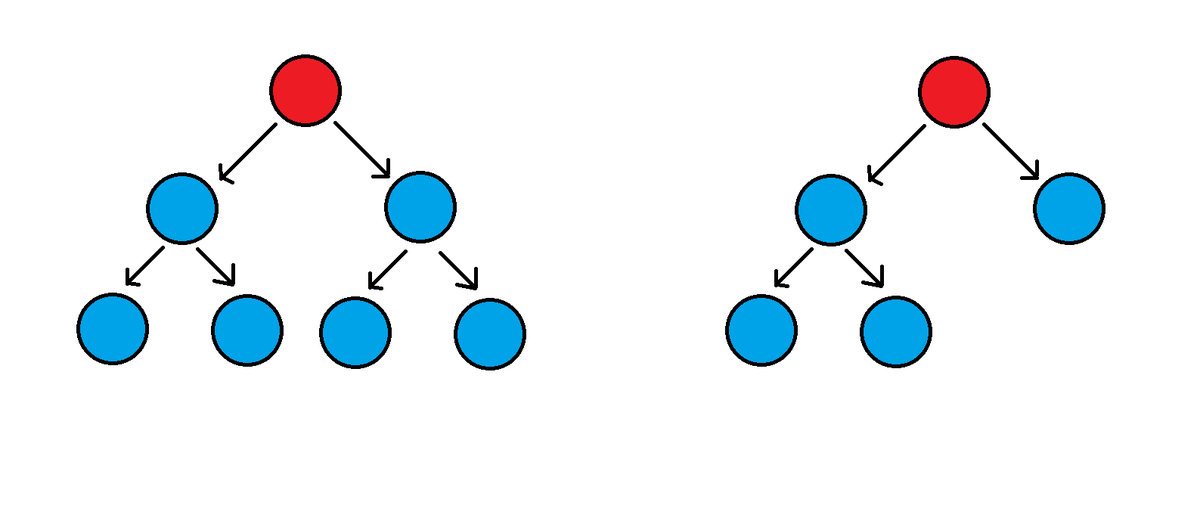
For example, as shown in the above left, you (red), as the apex founder, have $6$ (blue) members as the chain is complete. On the other hand, in the above right, you only have $4$ members as one of your members "drops off" or fails to find $2$ new members, as previously stated.

After some time, if you have $42$ members under your chain network, what is the least possible number of people who "drop off", according to this rule?

The answer is 2.

1 solution

Worranat Pakornrat
Apr 27, 2017

With the chain network, the number of members will be in terms $2^{n-1} + 2^{n-2} + \cdots + 4 + 2 = 2^n - 2$ , where $n$ is a positive integer for number of generations. In other words, with the whole network, there are theoretically $2^n - 1$ including the (red) founder, but if we exclude the founder and count only the (blue) members, there will be $2^n - 2$ .

Now by having someone to "drop off", the network will lose the amount of people in terms of $2^m - 2$ as any member can be considered as the "founder" for a smaller pyramid chain as well.

Hence, if $42$ members are present, the ideal whole chain should involve $2^6 - 2 = 62$ members, so $20$ members are missing.

Then since $20 = 14 + 6 = (2^4 - 2) + (2^3 - 2)$ , the least number of drops off happen at $2$ members, one at the third generation and another at the fourth.

Note that $20$ can not be written in terms of $2^m - 2$ . Thus, only one drop off can not lead to this scenario.

Therefore, the least number of drops off = $\boxed{2}$ .

Pyramid Selling

The answer is 2.

1 solution

0 pending reports