Pyramid vs Pyramid
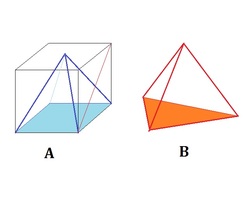 The square-based pyramid A is inscribed within a cube while the tetrahedral pyramid B has its sides equal to the square's diagonal (red) as shown.
The square-based pyramid A is inscribed within a cube while the tetrahedral pyramid B has its sides equal to the square's diagonal (red) as shown.
Which pyramid has more volume?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let x be the side length of the square.
The volume of pyramid A is simply one-third of the cube's volume: 3 x 3
The volume of pyramid B = 3 1 × B × H
The base B area is an equilateral triangle of x 2 : 4 3 [ x ( 2 ) ] 2 = 2 3 x 2
For height H, we can set right triangle OPQ, where O is a point directly below the pyramid's apex, P is the apex, and Q is one of the base points, as shown.
Then by taking a tetrahedron side PQ as the hypotenuse side of a right triangle, we can find H (OP) by Pythagorean theorem; all we need is to find the length of OQ. When dividing the triangular base area with 3 lines from point O to the other base points, the area will be divided into 3 equal areas. Therefore, the height of the divided triangle is also one third of the base height, making OQ two-thirds of the base height.
We know that the tetrahedral side equals to x 2 , so the base height = 2 3 x 2
Then OQ = 3 2 2 3 x 2 = 3 x ( 6 )
Hence, P Q 2 = O P 2 + O Q 2 ; H 2 = [ x ( 2 ) ] 2 - [ ( 3 x ( 6 ) ) ] 2 = 2 x 2 - 3 2 x 2 = 3 4 x 2
Thus, H = 3 2 x .
As a result, the volume of pyramid B = 3 1 2 3 x 2 3 2 x = 3 x 3 .
Therefore, the volume of pyramid B = volume of pyramid A = 3 x 3 .